如图，抛物线的顶点坐标为C（0，8），并且经过A（8，0），点P是抛物线上点A，C间的一个动点（含端点），过点P作直线y=8的垂线，垂足为点F，点D，E的坐标分别为（0，6），（4，0），连接PD

Question

如图，抛物线的顶点坐标为C（0，8），并且经过A（8，0），点P是抛物线上点A，C间的一个动点（含端点），过点P作直线y=8的垂线，垂足为点F，点D，E的坐标分别为（0，6），（4，0），连接PD，PE，DE．

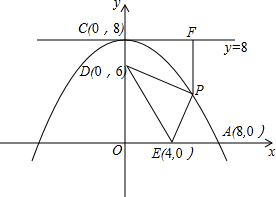
（1）求抛物线的解析式；
（2）猜想并探究：对于任意一点P，PD与PF的差是否为固定值？如果是，请求出此定值；如果不是，请说明理由；
（3）求：①当△PDE的周长最小时的点P坐标；②使△PDE的面积为整数的点P的个数．

Answer 1

（1）设抛物线的解析式为y=ax²+8．
∵经过点A（8，0），
∴64a+8=0，解得a=-(1)/(8)．
抛物线的解析式为：y=-(1)/(8)x²+8．
（2）PD与PF的差是定值．
理由如下：设P（a，-(1)/(8)a²+8），则F（a，8），
∵D（0，6），
∴PD=√(a2+((1)/(8)a2-2)2)=√(((1)/(8)a2+2)2)=(1)/(8)a²+2，PF=8-（-(1)/(8)a2+8）=(1)/(8)a2．
∴PD-PF=2．
（3）①当点P运动时，DE大小不变，则PE与PD的和最小时，△PDE的周长最小，
∵PD-PF=2，
∴PD=PF+2，
∴PE+PD=PE+PF+2，
∴当P、E、F三点共线时，PE+PF最小，此时点P，E的横坐标都为4，
∵将x=4代入y=-(1)/(8)x²+8，得y=6，
∴P（4，6），此时△PDE的周长最小．
②如图1所示：过点P做PH⊥x轴，垂足为H．

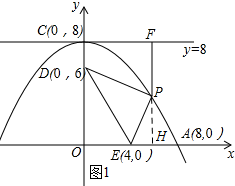
设P（a，-(1)/(8)a²+8）
∴PH=-(1)/(8)a²+8，EH=a-4，OH=a
S_△DPE=S_梯形PHOD-S_△PHE-S_△DOE=(1)/(2)a（-(1)/(8)a²+8+6）-(1)/(2)（-(1)/(8)a2+8）（a-4）-(1)/(2)×4×6=-(1)/(4)a²+3a+4=-(1)/(4)（a-6）²+13．
∵点P是抛物线上点A，C间的一个动点（含端点），
∴0≤a≤8，
∴当a=6时，S_△DPE取最大值为13．当a=0时，S_△DPE取最小值为4．即4≤S_△DPE≤13，其中，当S_△DPE=12时，有两个点P．
∴共有11个令S_△DPE为整数的点．