早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2-32x-2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值
题目详情
如图,抛物线y=ax2-
x-2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
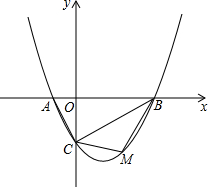
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
| 3 |
| 2 |

(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
▼优质解答
答案和解析
(1)将B(4,0)代入抛物线的解析式中,得:
0=16a-
×4-2,即:a=
;
∴抛物线的解析式为:y=
x2-
x-2.
(2)可得:B(4,0)、C(0,-2),设直线BC的解析式为:y=kx+b,
则
,
解得:
故直线BC的解析式为:y=x-2;
设xM=t,则yM=
t2-
t-2,yN=
t-2,
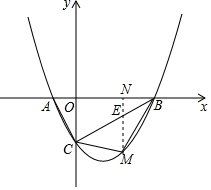
S△MBC=S△CME+S△BEM=
EM•ON+
EM•BN=
EM•OB
=
(
t-2-
t2+
t+2)×4
=-t2+4t
=-(t-2)2+4,
∴当t=2时,S△MBC=最大值为4,此时M(2,-3);
(3)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
0=16a-
| 3 |
| 2 |
| 1 |
| 2 |

∴抛物线的解析式为:y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)可得:B(4,0)、C(0,-2),设直线BC的解析式为:y=kx+b,
则
|
解得:
|
故直线BC的解析式为:y=x-2;
设xM=t,则yM=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
S△MBC=S△CME+S△BEM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=-t2+4t
=-(t-2)2+4,
∴当t=2时,S△MBC=最大值为4,此时M(2,-3);
(3)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
看了 如图,抛物线y=ax2-32...的网友还看了以下:
关于椭圆的规律,椭圆长轴端点两侧附近的圆弧是不是到长轴上某一点等距?如果存在,这点是焦点吗,不是的 2020-05-15 …
已知直线y=2/1x+3交x轴于A点,直线y=-2x+8交x轴于B点,两直线相交于C点,求△ABC 2020-05-23 …
(仅一道)中考数学题3若二次函数y=x^2+k与y=-x^2-3的图像的顶点重合,则下列结论不正确 2020-06-10 …
已知:点A(5,5)、B(-4,7)在X轴上有一点P,P点到A点和B点两点之间的距离之和最小,求这 2020-07-20 …
如图所示,可绕固定转轴B点转动的直木板OB与水平面间的倾斜角为θ,在直木板O点处用铰链连接一长度一 2020-07-31 …
(1/2)“直线y=1/2+2分别交x,y轴于点A,C.P点是该直线上在第一象限内的点,PB垂直x 2020-07-31 …
守恒物理题,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m, 2020-11-05 …
如图,在直线上两个相距1厘米的点A和B上各有一只电子青蛙.A点的青蛙沿直线跳往关于B点的对称点A1( 2020-12-23 …
如图,在直线上两个相距1厘米的点A和B上各有一只电子青蛙.A点的青蛙沿直线跳往关于B点的对称点A1( 2020-12-23 …
1.如图,已知在平面直角坐标系中,直线l:y=-x+2分别交两坐标轴于A、B两点(A点在y轴,B点交 2020-12-25 …