早教吧作业答案频道 -->数学-->
若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙
题目详情
若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是___(填空写所有正确选项的序号)
①y=
;②y=
;③y=
;④y=
.
①y=
| |
|
| |
|
| |
|
| |
|
▼优质解答
答案和解析
①函数y=-x-1,(x<0)关于原点对称的函数为-y=x-1,即y=-x+1,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数只有一个,所以函数f(x)的“伙伴点组”有1个,不满足条件.
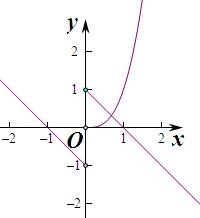
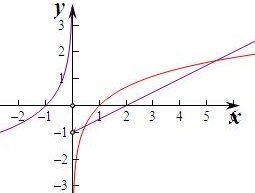
②函数y=-ln|x|(x<0)关于原点对称的函数为-y=-ln|-x|,即y=ln|x|,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.
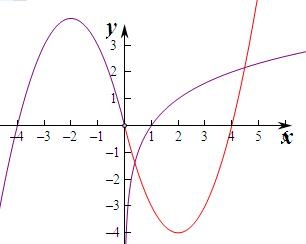
③函数y=-x2-4x,(x<0)关于原点对称的函数为-y=-x2+4x,即y=x2-4x,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.
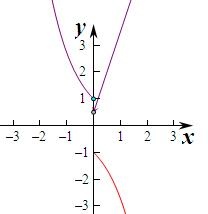
④函数y=e-x,(x<0)关于原点对称的函数为-y=ex,即y=-ex,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有0个,所以函数f(x)的“伙伴点组”有0个,不满足条件.
 ,
,
故答案为:②③.
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数只有一个,所以函数f(x)的“伙伴点组”有1个,不满足条件.
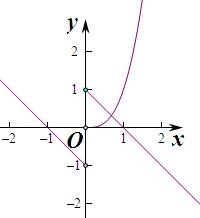
②函数y=-ln|x|(x<0)关于原点对称的函数为-y=-ln|-x|,即y=ln|x|,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.

③函数y=-x2-4x,(x<0)关于原点对称的函数为-y=-x2+4x,即y=x2-4x,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.

④函数y=e-x,(x<0)关于原点对称的函数为-y=ex,即y=-ex,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有0个,所以函数f(x)的“伙伴点组”有0个,不满足条件.
 ,
,故答案为:②③.
看了 若直角坐标平面内两点P,Q满...的网友还看了以下:
偶函数一定关于y轴对称吗、Y=F(X+8)为偶函数时图像关于X=8对称,为奇函数时关于点(8,0) 2020-04-06 …
下列说法中,不正确的是()A.图象关于原点对称的函数是奇函数B.奇函数的图象一定过原点C.图象关于 2020-04-26 …
已知函数y=xx−1,则下列四个命题中错误的是()A.该函数图象关于点(1,1)对称B.该函数的图 2020-05-13 …
命题“所有偶函数的图象关于y轴对称”的否定为()A.所有偶函数的图象不关于y轴对称B.存在偶函数的 2020-05-17 …
如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二 2020-06-30 …
一条一次函数的图像关于任何一条一次函数的图像对称后的直线的函数解析式的规律比如说y等于x加3关于y 2020-07-25 …
在我们学过的平面几何图形中(填一个就可以了)①有一条对称轴的图形有.②有二条对称轴的图形有.③有三 2020-08-02 …
当正N边形的N是奇数还是偶数的时候图形是轴对称图形?什么边数的图形既是中心对称又是轴对称. 2020-08-03 …
函数的对称函数y=-e^x的图象1.与y=e^x的图象关于y轴对称2.与y=e^x的图象关于坐标原点 2020-11-11 …
偶函数图像一定关于Y轴对称吗?奇函数图像一定关于原点对称吗?Y=F(X+8)为偶函数时图像关于X=8 2020-11-28 …