早教吧作业答案频道 -->数学-->
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(Ⅰ)证明MN∥平面PAB;(Ⅱ)求四面体N-BCM的体积.
题目详情
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
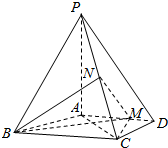
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求四面体N-BCM的体积.
▼优质解答
答案和解析
证明:(Ⅰ)取BC中点E,连结EN,EM,
∵N为PC的中点,∴NE是△PBC的中位线,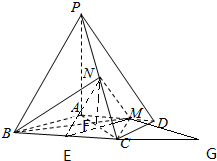
∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=
BC=AM=2,
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN⊂平面NEM,∴MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,
∵NF是△PAC的中位线,
∴NF∥PA,NF=
PA=2,
又∵PA⊥面ABCD,∴NF⊥面ABCD,
如图,延长BC至G,使得CG=AM,连结GM,
∵AM
CG,∴四边形AGCM是平行四边形,
∴AC=MG=3,
又∵ME=3,EC=CG=2,
∴△MEG的高h=
,
∴S△BCM=
×BC×h=
×4×
=2
,
∴四面体N-BCM的体积VN-BCM=
×S△BCM×NF=
×2
×2=
.
∵N为PC的中点,∴NE是△PBC的中位线,

∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE=
| 1 |
| 2 |
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN⊂平面NEM,∴MN∥平面PAB.
(Ⅱ)取AC中点F,连结NF,
∵NF是△PAC的中位线,
∴NF∥PA,NF=
| 1 |
| 2 |
又∵PA⊥面ABCD,∴NF⊥面ABCD,
如图,延长BC至G,使得CG=AM,连结GM,
∵AM
| ∥ |
. |
∴AC=MG=3,
又∵ME=3,EC=CG=2,
∴△MEG的高h=
| 5 |
∴S△BCM=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∴四面体N-BCM的体积VN-BCM=
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
4
| ||
| 3 |
看了 如图,四棱锥P-ABCD中,...的网友还看了以下:
在直角三角形ABC中,角A=90度,AB=3,TAN角B=三分之四,点P在BC边上,切BP=3以点 2020-04-11 …
已知椭圆C:(a>b>0)的长轴长为4,焦距为2.(I)求椭圆C的方程;(Ⅱ)过动点M(0,m)( 2020-05-15 …
已知集P={x|x=3的M次方分之N,m∈N,n∈N},且a,b∈p,求证a+b∈p,ab∈p 2020-05-16 …
已知抛物线y=x2-2ax+a2-2的顶点为A,P点在该抛物线的对称轴上,且在A点上方,PA=3. 2020-06-11 …
条件概率问题,已知P(A),P(B|A),P(C|A),能否求得P(C|A,B)?写错了,是已知P 2020-06-13 …
1,P(A)=0.4P(AB)=0.2P(A|B)+P(A非|B非)=1求P(A并B)2,证明若P 2020-06-14 …
P(A)=0.7,P(A-B)=0.3.求P(A∪B).主要是P(AB)怎么求.已知时间A、B.P 2020-07-22 …
已知A(-1/2,0),B是圆F(x-1/2)2+y2=4,上一点,线段已知A(-1/2,0)B是 2020-08-03 …
对下表的分析不合理的是()分泌蛋白的肽链组成能否进入内质网能否分泌正常肽段P+肽段A能能异常肽段P+ 2020-12-09 …
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C(1)求抛物线的 2021-01-12 …