早教吧作业答案频道 -->数学-->
如图,在正三棱柱ABC-A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证:(1)直线A1E∥平面ADC1;(2)直线EF⊥平面ADC1.
题目详情
如图,在正三棱柱ABC-A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证:
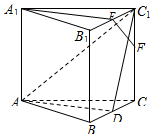
(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1.

(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1.
▼优质解答
答案和解析
证明:(1)连接ED,∵D,E分别为BC,B1C1的中点,
∴B1E∥BD且B1E=BD,
∴四边形B1BDE是平行四边形,
∴BB1∥DE且BB1=DE,又BB1∥AA1且BB1=AA1,
∴AA1∥DE且AA1=DE,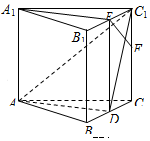
∴四边形AA1ED是平行四边形,
∴A1E∥AD,又∵A1E⊄平面ADC1,AD⊂平面ADC1,
∴直线A1E∥平面ADC1.
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,
又AD⊂平面ABC,所以AD⊥BB1,
又△ABC是正三角形,且D为BC的中点,∴AD⊥BC,
又BB1,BC⊂平面B1BCC1,BB1∩BC=B,
∴AD⊥平面B1BCC1,
又EF⊂平面B1BCC1,∴AD⊥EF,
又EF⊥C1D,C1D,AD⊂平面ADC1,C1D∩AD=D,
∴直线EF⊥平面ADC1.
∴B1E∥BD且B1E=BD,
∴四边形B1BDE是平行四边形,
∴BB1∥DE且BB1=DE,又BB1∥AA1且BB1=AA1,
∴AA1∥DE且AA1=DE,

∴四边形AA1ED是平行四边形,
∴A1E∥AD,又∵A1E⊄平面ADC1,AD⊂平面ADC1,
∴直线A1E∥平面ADC1.
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,
又AD⊂平面ABC,所以AD⊥BB1,
又△ABC是正三角形,且D为BC的中点,∴AD⊥BC,
又BB1,BC⊂平面B1BCC1,BB1∩BC=B,
∴AD⊥平面B1BCC1,
又EF⊂平面B1BCC1,∴AD⊥EF,
又EF⊥C1D,C1D,AD⊂平面ADC1,C1D∩AD=D,
∴直线EF⊥平面ADC1.
看了 如图,在正三棱柱ABC-A1...的网友还看了以下:
本初子午线是()A.东西半球的分界线B.东西方向的起点线C.南北半球的分界线D.东西经度的分界线 2020-04-23 …
已知曲线C的方程为y2=4x(x>0),曲线E是以F1(-1,0)、F2(1,0)为焦点的椭圆,点 2020-05-15 …
如图直线y=-3/4+8分别交x轴,y轴于A,B两点,线段A,B垂直平分线C,E分别交于x轴y轴于 2020-05-16 …
1.点A,C,E共线,△ABC和△DCE为等边三角形.求证PQ∥AE. 2020-05-17 …
已知Rt三角形ABC,斜边上的高为CD,E是BC上的一点,过C,E,D三点所作的圆交AE於F,求证 2020-06-03 …
如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,E在同一条直线上,连接BD,求BD² 2020-06-27 …
如图,已知点B,C,E在一直线上,△ABC,△DCE都是等边三角形,联结AE,BD,试说明△ACE 2020-06-27 …
l1平行于l2,点A,D在l1上,点B,C,E,F在l2上,已知BC=3,EF=8,三角形ABC的 2020-07-13 …
已知点M(-1,0),N(1,0),曲线E上任意一点到M的距离均是到点N距离的3倍.(1)求曲线E的 2020-11-27 …
如图△abc与△cde都是等边三角形,且点A.C.E在同一条直线上,AD与BC交与点M,BE与CD交 2021-01-10 …