早教吧作业答案频道 -->数学-->
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C(1)求证:平面ABC1⊥平面A1ACC1(2)设D是A1C1的中点,判断并证明在线段BB1上是否存在点E,使DE∥平面AB
题目详情
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C
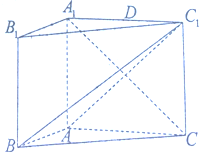
(1)求证:平面ABC1⊥平面A1ACC1
(2)设D是A1C1的中点,判断并证明在线段BB1上是否存在点E,使DE∥平面ABC1,若存在,求点E到平面ABC1的距离.

(1)求证:平面ABC1⊥平面A1ACC1
(2)设D是A1C1的中点,判断并证明在线段BB1上是否存在点E,使DE∥平面ABC1,若存在,求点E到平面ABC1的距离.
▼优质解答
答案和解析
(1)证明:在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,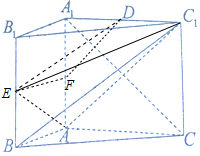
∴AA1⊥AB,又AA1⊥BC,AB∩BC=B,
∴AA1⊥平面ABC,
∴AA1⊥AC,又AA1=AC,∴A1C⊥AC1,
又BC1⊥A1C,BC1∩AC1=C1,
∴A1C⊥平面ABC1,又A1C⊂平面A1ACC1,
∴平面ABC1⊥平面A1ACC1 ;
(2) 当E为BB1的中点时,连接AE,EC1,DE,
如图,取AA1的中点F,连接EF,FD,
∵EF∥AB,DF∥AC1,
又EF∩DF=F,AB∩AC1=A,
∴平面EFD∥平面ABC1,又DE⊂平面EFD,
∴DE∥平面ABC1,
又∵VE-ABC1=VC1-ABE,C1A1⊥平面ABE,
设点E到平面ABC1 的距离为d,
∴
×
×2×4
×d=
×
×2×2×4,得d=
,
∴点E到平面ABC1的距离为
.

∴AA1⊥AB,又AA1⊥BC,AB∩BC=B,
∴AA1⊥平面ABC,
∴AA1⊥AC,又AA1=AC,∴A1C⊥AC1,
又BC1⊥A1C,BC1∩AC1=C1,
∴A1C⊥平面ABC1,又A1C⊂平面A1ACC1,
∴平面ABC1⊥平面A1ACC1 ;
(2) 当E为BB1的中点时,连接AE,EC1,DE,
如图,取AA1的中点F,连接EF,FD,
∵EF∥AB,DF∥AC1,
又EF∩DF=F,AB∩AC1=A,
∴平面EFD∥平面ABC1,又DE⊂平面EFD,
∴DE∥平面ABC1,
又∵VE-ABC1=VC1-ABE,C1A1⊥平面ABE,
设点E到平面ABC1 的距离为d,
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
∴点E到平面ABC1的距离为
| 2 |
看了 如图,在三棱柱ABC-A1B...的网友还看了以下:
在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.(Ⅰ)求证:B1E⊥AD1;( 2020-05-16 …
棱长为1的正方体ABCD-A1B1C1D1的8个顶分别是棱AA1,DD1的中点,则直线EF被球棱长 2020-05-16 …
追分追分1、已知A(3,5,2)B(-1,3,4)C(1,1,1)把向量AB按向量(2,1,1)平 2020-06-09 …
已知正三棱柱ABC-A1B1C1中,棱AA1=AB=a,且D,E分别为棱AA1,B1C1的中点.1 2020-07-12 …
已知正三棱柱ABC-A1B1C1中,棱AA1=AB=a,且D,E分别为棱AA1,B1C1的中点.1 2020-07-12 …
若二面角α-l-β是直二面角,A∈α,B∈β,AA1⊥L于A1,BB1⊥L于B1,AA1=A1B1 2020-08-02 …
在直三棱柱ABC-A1B1C1中,AC=AA1=2,∠ACB=90°,点E,F分别是棱AB,BB1 2020-08-02 …
已知平行六面体ABCD-A1B1C1D1的底面边长为a的正方形;侧棱AA1的长为b,且∠AA1B1 2020-08-03 …
如图所示已知△ABC的面积S=1在图1中若AA1/AB=BB1/BC=CC1/CA=1/2如图,已知 2020-10-31 …
已知△ABC中,AB=AC,∠BAC=45°,绕点C顺时针旋转△ABC,使点B落在AB边上,得△A1 2020-10-31 …