早教吧作业答案频道 -->数学-->
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.(1)求证:EF∥平面PAB;(2)若AP=AD,且平面PAD⊥平面ABCD,证明:AF⊥平面PCD.
题目详情
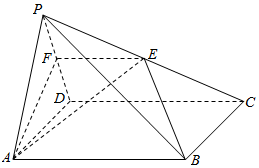
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E、F分别是棱PC和PD的中点.
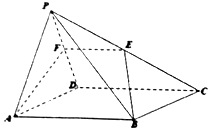
(1)求证:EF∥平面PAB;
(2)若AP=AD,且平面PAD⊥平面ABCD,证明:AF⊥平面PCD.

(1)求证:EF∥平面PAB;
(2)若AP=AD,且平面PAD⊥平面ABCD,证明:AF⊥平面PCD.
▼优质解答
答案和解析
 (本题满分为12分)
(本题满分为12分)
(1)证明:因为点E、F分别是棱PC和PD的中点,
所以CD∥EF.
因为底面ABCD是矩形,
所以AB∥CD.可得:AB∥EF,
又因为EF⊄平面PAB,AB⊂平面PAB,
所以EF∥平面PAB.…(6分)
(2)证明:在矩形ABCD中,CD⊥AD.
又因为平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
所以CD⊥平面PAD.
又AF⊂平面PAD,
所以CD⊥AF.
由(1)可知AB∥EF,
又因为AB∥CD,所以CD∥EF.由点E是棱PC中点,所以点F是棱PD中点.
在△PAD中,因为PA=AD,所以AF⊥PD.
又因为PD∩CD=D,所以AF⊥平面PCD.…(12分)
 (本题满分为12分)
(本题满分为12分)(1)证明:因为点E、F分别是棱PC和PD的中点,
所以CD∥EF.
因为底面ABCD是矩形,
所以AB∥CD.可得:AB∥EF,
又因为EF⊄平面PAB,AB⊂平面PAB,
所以EF∥平面PAB.…(6分)
(2)证明:在矩形ABCD中,CD⊥AD.
又因为平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
所以CD⊥平面PAD.
又AF⊂平面PAD,
所以CD⊥AF.
由(1)可知AB∥EF,
又因为AB∥CD,所以CD∥EF.由点E是棱PC中点,所以点F是棱PD中点.
在△PAD中,因为PA=AD,所以AF⊥PD.
又因为PD∩CD=D,所以AF⊥平面PCD.…(12分)
看了 如图,在四棱锥P-ABCD中...的网友还看了以下:
平行四边形ABCD中ac^2+bd^2=2ab^2类比到平行六面体ABCD-A'B'C'D'是什么 2020-05-13 …
正方体ABCD-A'B'C'D'的棱长为8,M.N.P分别是A'B',AD,BB'的中点.(1)画 2020-05-16 …
立方体ABCD-A'B'C'D',B'D'中点为O,求AC与DD' AC与D'C' AC与B'D' 2020-05-16 …
现有A,B,C,D四种物质,已知A,B为黑色粉末,C,D为无色气体,A,B在高温下作用能生成D,A 2020-05-17 …
用五种颜料给一下4区域染色,每个区域用一种颜色,且相邻区域不能同色,有多少种不同的染法?A与B、D 2020-06-03 …
左下图为一阶梯截面,老鼠沿两边A-B-D的路线逃跑,猫同时沿阶梯(折线)A-C-D的路线去追,结果 2020-06-20 …
已知::有四个人A,B,C,D各自带一顶帽子,其中有2个红色,2个黄色现在有一堵墙,A坐在墙的左面 2020-06-26 …
分子分母比例相同的两个分数,让它们分子减分子,分母减分母,得到的比例还一样吗,这个定理叫什么名字? 2020-07-18 …
1.若平行四边形ABCD相似于平行四边形A'B'C'D',平行四边形ABCE的面积:平行四边形A' 2020-08-01 …
在正方体ABCD-A’B’C’D’中,E,F分别是棱C’D’,B’C’的中点,O是底面A’B’C’ 2020-08-03 …