早教吧作业答案频道 -->数学-->
已知椭圆的左右焦点分别为F1,F2,短轴两个端点为A,B,且四边形F1AF2B是边长为2的正方形.(I)求椭圆方程;(II)若C,D分别是椭圆长轴的左右端点,动点M满足MD⊥CD,连接CM,交椭圆于
题目详情
已知椭圆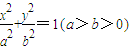 的左右焦点分别为F1,F2,短轴两个端点为A,B,且四边形F1AF2B是边长为2的正方形.
的左右焦点分别为F1,F2,短轴两个端点为A,B,且四边形F1AF2B是边长为2的正方形.
(I)求椭圆方程;
(II)若C,D分别是椭圆长轴的左右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.求证: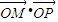 为定值.
为定值.
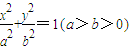 的左右焦点分别为F1,F2,短轴两个端点为A,B,且四边形F1AF2B是边长为2的正方形.
的左右焦点分别为F1,F2,短轴两个端点为A,B,且四边形F1AF2B是边长为2的正方形.(I)求椭圆方程;
(II)若C,D分别是椭圆长轴的左右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.求证:
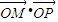 为定值.
为定值.▼优质解答
答案和解析
【答案】分析:(1)利用椭圆的几何性质求出a、b的值,从而写出标准方程.(2)设M(2,y),写出直线CM的方程,并把它代入椭圆的方程,可求P的坐标,进而得到向量OM、OP的坐标,计算这2个向量坐标的数量积,得出定值.(1)∵左右焦点分别为F1,F2,短轴两个端点为A,B,且四边形F1AF2B是边长为2的正方形,∴a=2,b=c,a2=b2+c2,∴b2=2,∴椭圆方程为.(4分)(2)C(-2,0),D(2,0),设M(2,y),P(x1,y1),则.直线CM:y-0=(x-2),即 .(6分)代入椭圆x2+2y2=4,得,故次方程的两个根分别为-2和x1,(8分)由韦达定理可得x1-2=,∴,∴.∴,(10分)∴+==4 (定值).(12分)点评:本题考查椭圆的标准方程的求法、2个向量的数量积公式的应用,及一元二次方程根与系数的关系,属于中档题.
看了 已知椭圆的左右焦点分别为F1...的网友还看了以下:
求椭圆方程设椭圆的中心在原点,坐标轴为对称轴,一个焦点与短轴两端点的连线互相垂直,且此焦点与长轴上 2020-05-15 …
椭圆的中心在原点,焦点在X轴,若椭圆的一个焦点将长轴分成的两段的比例中项等于椭圆的焦距,又已知直线 2020-05-15 …
椭圆的中心在原点,焦点在x轴上,若椭圆的一个焦点将长轴分成的两段的比例中项等于椭圆的焦距,又已知直 2020-05-15 …
已知椭圆的中心在原点,焦点在x轴,从焦点看短轴的两个端点.已知椭圆的中心在原点,焦点在x轴,从焦点 2020-05-16 …
(1/2)椭圆的中心点在原点,焦点在X轴上,一个焦点与短轴两个端点的连线互相垂直,且此焦点与长轴上 2020-05-16 …
数学椭圆问题1.已知椭圆X^2/144+y^2/25=1和直线l:y=x+m,若圆上存在两点A、B 2020-06-21 …
已知椭圆C:(a>b>0)的一个焦点到长轴的两个端点的距离分别为和.(1)求椭圆的方程;(2)若过 2020-07-30 …
若椭圆的短轴长是4,X轴上的一个焦点与短轴的两个端点连线之间的夹角为60度,则该椭圆的标准方程是( 2020-07-31 …
椭圆的中心在原点,焦点在x轴上,一个焦点与短轴两端点的连线互相垂直,且这个焦点到长轴上较近的端点的 2020-07-31 …
椭圆求标准方程!设椭圆的中心在原点,坐标为对称轴,一个焦点与短轴的连线互相垂直,且此焦点与长轴上较 2020-08-02 …