早教吧作业答案频道 -->数学-->
如图,四边形ABCD外切于O,切点分别是E、F、G、H.(1)请探索四边形ABCD四边AB、BC、CD、AD之间的关系;(2)圆的外切平行四边形是形;(3)圆的外切矩形是形;(4)若AB:BC:CD:DA=1
题目详情
如图,四边形ABCD外切于 O,切点分别是E、F、G、H.
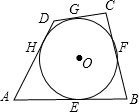
(1)请探索四边形ABCD四边AB、BC、CD、AD之间的关系;
(2)圆的外切平行四边形是___形;
(3)圆的外切矩形是___形;
(4)若AB:BC:CD:DA=1:3:4:x,且四边形ABCD的周长为20cm,则x=___,AD=___.

(1)请探索四边形ABCD四边AB、BC、CD、AD之间的关系;
(2)圆的外切平行四边形是___形;
(3)圆的外切矩形是___形;
(4)若AB:BC:CD:DA=1:3:4:x,且四边形ABCD的周长为20cm,则x=___,AD=___.
▼优质解答
答案和解析
(1)∵四边形ABCD外切于 O,切点分别是E、F、G、H,
∴AH=AE,BE=BF,CF=CG,DG=DH,
∴AH+DH+CF+BF=DG+CG+AE+BE,
即AD+BC=AB+DC;
(2)由(1)得,圆的外切四边形对边和相等,
则圆的外切平行四边形是:菱形;
故答案为:菱;
(3)由(1)得,圆的外切四边形对边和相等,
则圆的外切矩形是正方形;
故答案为:正方;

(4)∵AB:BC:CD:DA=1:3:4:x,AD+BC=AB+DC,
∴1+4=3+x,
则x=2,
∵四边形ABCD的周长为20cm,
∴20÷(1+3+4+2)=2,
∴AD=2×2=4(cm).
故答案为:2,4cm.
∴AH=AE,BE=BF,CF=CG,DG=DH,
∴AH+DH+CF+BF=DG+CG+AE+BE,
即AD+BC=AB+DC;
(2)由(1)得,圆的外切四边形对边和相等,
则圆的外切平行四边形是:菱形;
故答案为:菱;
(3)由(1)得,圆的外切四边形对边和相等,
则圆的外切矩形是正方形;
故答案为:正方;

(4)∵AB:BC:CD:DA=1:3:4:x,AD+BC=AB+DC,
∴1+4=3+x,
则x=2,
∵四边形ABCD的周长为20cm,
∴20÷(1+3+4+2)=2,
∴AD=2×2=4(cm).
故答案为:2,4cm.
看了 如图,四边形ABCD外切于O...的网友还看了以下:
1)解关于x的方程:x^2+3bx-a^2+ab+2b^2=02)(√a+1+√a-1)/(√a+ 2020-06-09 …
(1)在直角坐标系中,将坐标为(1,1),(2,1),(2,2),(1,2),(1,3),(2,3 2020-06-14 …
关于形容词和副词的基础,想问下.1:关于形容词IhavefishaliveIhavelovelyf 2020-07-24 …
下列命题中,其中正确的个数有()1、设A、B关于直线MN对称,则AB垂直平分MN2、线段的两个端点 2020-07-30 …
双曲线斜率问题三角形PQR是正3角型.P为定点(1.0)、QR关于X轴对称.且都在X=1左侧.若Q 2020-07-30 …
下列说法中,正确的是()A.关于某直线对称的两个三角形是全等三角形B.全等三角形是关于某直线对称的 2020-07-31 …
将△ABC的三个顶点的横坐标不变,纵坐标乘以-1,则所得图形()A.与原图形关于x轴对称B.与原图 2020-07-31 …
将△ABC的三个顶点的横坐标乘以−1,纵坐标不变,则所得图形()。A.与原图形关于y轴对称B.与原 2020-07-31 …
用配方法将关于x的方程x2+5x+n=0可以变形为(x+p)2=9,那么用配方法也可以将关于x的方程 2020-10-31 …
关于以下成语中的“影”,形成的光学原理相同的是()(1)形影不离(2)湖光倒影(3)毕业合影(4)关 2020-12-25 …