早教吧作业答案频道 -->数学-->
已知正方形ABCD中,点E、F分别为BC、CD上的点,连接AE,BF相交于点H,且AE⊥BF.(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH
题目详情
已知正方形ABCD中,点E、F分别为BC、CD上的点,连接AE,BF相交于点H,且AE⊥BF.
(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;
(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;
(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.
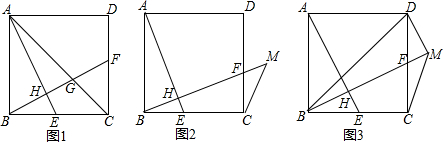
(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;
(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;
(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠BCD=90°,
∴∠ACB=∠ACD=45°,
∵AE⊥BF,
∴∠AEB+∠FBC=90°,
∵∠FBC+∠BFC=90°
∴∠AEB=∠BFC,
∵∠AGF=∠BFC+∠ACF,
∴∠AGF=∠AEB+45°;
(2) 过C作CK⊥BM于K,
∴∠BKC=90°,
∵∠BMC=45°,
∴CK=MK,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABH=∠BCK,
在△ABH与△BCK中,
,
∴△ABH≌△BCK,
∴BH=CK=MK,AH=BK,
∴BM=BK+MK=AH+BH;
(3) 由(2)得,BH=CK=BH,
∵H为BM的三等分点,
∴BH=HK=KM,
过E作EN⊥CK于N,
∴四边形HENK是矩形,
∴HK=EN=BH,∠BHE=∠NEC,
在△BHE与△ENC中,
,
∴△BHE≌△ENC,
∴HE=CN=NK=1,
∴CK=BH=2,
∴BM=6,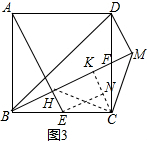
连接CH,
∵HK=MK,CK⊥MH,∠BMC=45°,
∴CH=CM,∠MCH=90°,
∴∠BCH=∠DCM,
在△BHC与△DMC中,
,
∴△BHC≌△DMC,
∴BH=DM=2,∠BHC=∠DMC=135°
∴∠DMB=90°,
∴△BDM的面积=6.
∴∠ABC=∠BCD=90°,
∴∠ACB=∠ACD=45°,
∵AE⊥BF,
∴∠AEB+∠FBC=90°,
∵∠FBC+∠BFC=90°
∴∠AEB=∠BFC,
∵∠AGF=∠BFC+∠ACF,
∴∠AGF=∠AEB+45°;
(2) 过C作CK⊥BM于K,
∴∠BKC=90°,
∵∠BMC=45°,
∴CK=MK,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABH=∠BCK,
在△ABH与△BCK中,
|
∴△ABH≌△BCK,
∴BH=CK=MK,AH=BK,
∴BM=BK+MK=AH+BH;
(3) 由(2)得,BH=CK=BH,
∵H为BM的三等分点,
∴BH=HK=KM,
过E作EN⊥CK于N,
∴四边形HENK是矩形,
∴HK=EN=BH,∠BHE=∠NEC,
在△BHE与△ENC中,
|
∴△BHE≌△ENC,
∴HE=CN=NK=1,
∴CK=BH=2,
∴BM=6,

连接CH,
∵HK=MK,CK⊥MH,∠BMC=45°,
∴CH=CM,∠MCH=90°,
∴∠BCH=∠DCM,
在△BHC与△DMC中,
|
∴△BHC≌△DMC,
∴BH=DM=2,∠BHC=∠DMC=135°
∴∠DMB=90°,
∴△BDM的面积=6.
看了 已知正方形ABCD中,点E、...的网友还看了以下:
a,b,c且a<b<c,试找出它们的共同点,并证明你的结论.a=3,b=4,c=5(3^2+4^2= 2020-03-30 …
tanA/tanB=(2c-b)/b.tanA/tanB=(2c-b)/b.sinA*cosB/( 2020-04-09 …
已知abc是三角形abc的三边长,且满足a^2*c^2-b^2*c^2=a^4-b^4判断三角形a 2020-06-08 …
20.x^2/a^2+y^2/b^2+z^2/c^2=1成立;20.x^2/a^2+y^2/b^2 2020-06-11 …
因式分解:a^2(m-b)(m-c)(c-b)+b^2(m-c)(m-a)(a-c)+c^2(m- 2020-06-12 …
利用(a+b+c)^2=a^2+b^2^c^2+2ab+2ac+abc,推导(a+b+c)^2+a 2020-07-30 …
3角形3边abc求证:abc≥(a+b-c)(a+c-b)(b+c-a)假设x=a+b-c>0y=a 2020-11-01 …
aW、bX、cC、dZ、eR是五种短周期元素,e-d=d-c=c-b=b-a=4,其中一种是常见金属 2020-11-26 …
近世代数2、设A,B是U的子集,规定A+B=(A-B)(B-A).证明:(1)A+B=B+A(2)A 2020-11-28 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …