早教吧作业答案频道 -->数学-->
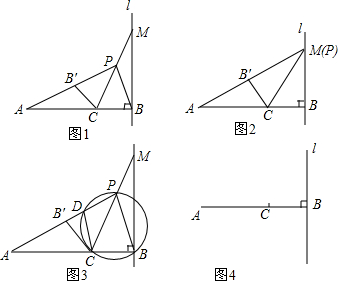
如图1,直线l⊥AB于点B,点C在AB上,且AC:CB=2:1,点M是直线l上的动点,作点B关于直线CM的对称点B′,直线AB′与直线CM相交于点P,连接PB.(1)如图2,若点P与点M重合,则∠PAB=,线段PA
题目详情
如图1,直线l⊥AB于点B,点C在AB上,且AC:CB=2:1,点M是直线l上的动点,作点B关于直线CM的对称点B′,直线AB′与直线CM相交于点P,连接PB.
(1)如图2,若点P与点M重合,则∠PAB=___,线段PA与PB的比值为___
(2)如图3,若点P与点M不重合,设过P,B,C三点的圆与直线AP相交于D,连接CD,求证:①CD=CB′;②PA=2PB;
(3)如图4,若AC=2,BC=1,则满足条件PA=2PB的点都在一个确定的圆上,在以下小题中选做一题:
①如果你能发现这个确定的圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB;
②如果你不能发现这个确定的圆的圆心和半径,那么请取出几个特殊位置的P点,如点P在直线AB上,点P与点M重合等进行探究,求这个圆的半径.
(1)如图2,若点P与点M重合,则∠PAB=___,线段PA与PB的比值为___
(2)如图3,若点P与点M不重合,设过P,B,C三点的圆与直线AP相交于D,连接CD,求证:①CD=CB′;②PA=2PB;
(3)如图4,若AC=2,BC=1,则满足条件PA=2PB的点都在一个确定的圆上,在以下小题中选做一题:
①如果你能发现这个确定的圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB;
②如果你不能发现这个确定的圆的圆心和半径,那么请取出几个特殊位置的P点,如点P在直线AB上,点P与点M重合等进行探究,求这个圆的半径.

▼优质解答
答案和解析
(1) 如图2,
∵B关于直线CM的对称点为点B′,
∴△PBC沿PC翻折得到△PB′C,
∴CB′=CB,∠PB′C=∠PBC=90°,
∵AC:CB=2:1,
∴AC=2CB′,
在Rt△AB′C中,sin∠A=
=
,
∴∠A=30°,
在Rt△PAB中,PA=2PB;
故答案为30°;2;
(2)证明:①∵B关于直线CM的对称点为点B′,
∴△PBC沿PC翻折得到△PB′C,
∴∠PB′C=∠PBC,
∵∠CDB′=∠CBP,
∴∠CDB′=∠CB′D,
∴CD=CB′;
②作B′E∥PC交AC于E,连结BB′交PC于F,如图3,
∵B关于直线CM的对称点为点B′,
∴FB=FB′,PB=PB′,
而CF∥B′E,
∴BC=CE,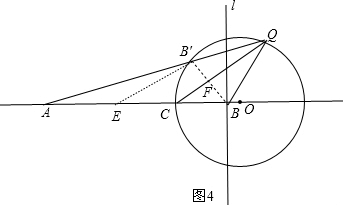
∵AC=2BC,
∴AE=EC,
而B′E∥PC,
∴AB′=PB′,
∴PA=2PB′=2PB;
(3)选①.
证明:作B′E∥QC交AC于E,连结BB′交QC于F,如图4,
∵B关于直线CM的对称点为点B′,
∴FB=FB′,QB=QB′,
而CF∥B′E,
∴BC=CE,
∵AC=2BC,
∴AE=EC,
而B′E∥QC,
∴AB′=QB′,
∴QA=2QB′=2QB.

∵B关于直线CM的对称点为点B′,
∴△PBC沿PC翻折得到△PB′C,
∴CB′=CB,∠PB′C=∠PBC=90°,
∵AC:CB=2:1,
∴AC=2CB′,
在Rt△AB′C中,sin∠A=
| CB′ |
| AC |
| 1 |
| 2 |
∴∠A=30°,
在Rt△PAB中,PA=2PB;
故答案为30°;2;
(2)证明:①∵B关于直线CM的对称点为点B′,
∴△PBC沿PC翻折得到△PB′C,
∴∠PB′C=∠PBC,
∵∠CDB′=∠CBP,
∴∠CDB′=∠CB′D,
∴CD=CB′;
②作B′E∥PC交AC于E,连结BB′交PC于F,如图3,
∵B关于直线CM的对称点为点B′,
∴FB=FB′,PB=PB′,
而CF∥B′E,
∴BC=CE,

∵AC=2BC,
∴AE=EC,
而B′E∥PC,
∴AB′=PB′,
∴PA=2PB′=2PB;
(3)选①.
证明:作B′E∥QC交AC于E,连结BB′交QC于F,如图4,
∵B关于直线CM的对称点为点B′,
∴FB=FB′,QB=QB′,
而CF∥B′E,
∴BC=CE,
∵AC=2BC,
∴AE=EC,
而B′E∥QC,
∴AB′=QB′,
∴QA=2QB′=2QB.
看了 如图1,直线l⊥AB于点B,...的网友还看了以下:
关于轨迹的数学题已知点A(0,1),定直线L:y=-1,B为L上的一个动点.过B作直线m垂直于L, 2020-04-25 …
(2009•塘沽区一模)如图,在△ABC中AC=BC,∠ACB=90°,以BC为直径作⊙O,连接O 2020-05-13 …
已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点, 2020-05-13 …
平面直角坐标系中,A(4,8)、C(0,6),过A点作AB⊥x轴于B,平面直角坐标系中,A(4,8 2020-05-15 …
83页同济6有句{如果函数在开区间ab上可导,且在a点右连续,b点作连续.就说在闭区间ab上连续. 2020-08-01 …
已知等腰直角三角形ABC中,D为斜边BC上一点,过D点作DE⊥BC交AB于E,连接CE,F为CE中 2020-08-03 …
如图,在平面直角坐标系xOy中,抛物线的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点 2020-11-01 …
已知直线l同旁的两点A、B,在l上求一点P,使PA+PB最小,则求P点的作法正确的为()A.作A关于 2020-11-06 …
(如图)已知线段AB的端点A平移到位置C,作出线段AB平移后的图形.作法(1):连结AC,再过B点作 2020-11-06 …
在平面直角坐标系中,已知A(-1.0)B(0.2)点C在第二象限,CD⊥x轴,垂足为D,且△CDA≌ 2021-01-22 …