早教吧作业答案频道 -->数学-->
如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.(1)求证:①△OAC≌△OBD,②∠AEB=60°;(2)连结OE,OE是否平分∠AED?请说明理由.
题目详情
如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
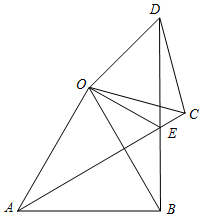
(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.

(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.
▼优质解答
答案和解析
(1)证明:①∵△OAB与△OCD都是等边三角形,
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
∴△OAC≌△OBD.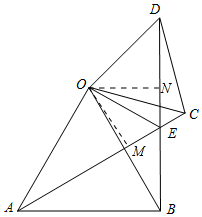
②∵△OAC≌OBD,
∴∠OAE=∠OBD,
∵△OAB是等边三角形,
∴∠OAB+∠OBA=120°,
∴∠OAE+∠BAE+∠OBA=120°,
即∠EAB+∠EBA=120°,
∴∠AEB=60°.
(2) OE平分∠AED.理由如下:
作OM⊥AC于M,ON⊥BD于N.
∵△OAC≌△OBD,
∴S△OAC=S△OBD,
∴
•AC•OM=
•BD•ON,
∴OM=ON,
∴OE平分∠AED.
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
∴△OAC≌△OBD.

②∵△OAC≌OBD,
∴∠OAE=∠OBD,
∵△OAB是等边三角形,
∴∠OAB+∠OBA=120°,
∴∠OAE+∠BAE+∠OBA=120°,
即∠EAB+∠EBA=120°,
∴∠AEB=60°.
(2) OE平分∠AED.理由如下:
作OM⊥AC于M,ON⊥BD于N.
∵△OAC≌△OBD,
∴S△OAC=S△OBD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴OM=ON,
∴OE平分∠AED.
看了 如图,△OAB与△OCD都是...的网友还看了以下:
春分日,当0°经线为0点时,某地北边是热带,南边是温带,西边是黑夜,东边是白昼,该地的地理坐标() 2020-05-04 …
已知抛物线Y=aX2+bx+c经过点A(0,3)B(1,0) C(5,0)三点 1.求抛物线解析式 2020-05-15 …
如图,多边形ABCDEF的顶点坐标为A(-2,2)B(-2,-2),C(4,-2),D(4,0)E 2020-05-16 …
微分方程y"+y'=2x^2e^x的特解应设为y*=A.(Ax^2+Bx+C)e^xB.(Ax^3 2020-05-22 …
1.平面直角坐标系中,多边形ABCDEF的各个顶点的坐标分别是A(1,0)B(2,3)C(5,6) 2020-07-09 …
五元一次方程的解法0.01349/[e+0.6842(1-e)]=a0.8638/[e+0.565 2020-07-16 …
如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半 2020-07-21 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
y+c=x+bc,b都是常数他们都不等于0.现在问2个基础的问题,假如他们2边用1除,是变成1/(y 2020-11-20 …
初二一次函数已知如图,△ABC的顶点坐标分别为A(0,2),B(-2,0),C(1,0)O是坐标原点 2020-12-08 …