早教吧作业答案频道 -->数学-->
如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.证明:DM•KE=DN•KF.
题目详情
如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.
证明:DM•KE=DN•KF.
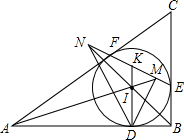
证明:DM•KE=DN•KF.

▼优质解答
答案和解析
证明:连接IE,如图所示: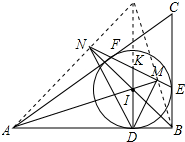
∵△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,
∴ID⊥AB,IE⊥BC,
∴∠IDB=∠IEB=90°,
∴∠IDB+∠IEB=180°,
∴I,D,B,E四点共圆.
又∵∠AID=90°-∠IAD,∠MED=∠FDA=90°-∠IAD,
∴∠AID=∠MED,
∴I,D,E,M四点共圆.
∴I,D,B,E,M五点共圆,∠IMB=∠IEB=90°,
即AM⊥BM.
同理,I,D,A,N,F五点共圆,且BN⊥AN.
设直线AN,BM交于点G,则点I为△GAB的垂心.又ID⊥AB,
∴G,I,D共线.
∵G,N,D,B四点共圆,
∴∠ADN=∠G.
同理∠BDM=∠G.
∴DK平分∠MDN,
∴
=
①.
又由I,D,E,M;I,D,N,F分别共圆,
∴KM•KE=KI•KD=KF•KN,
∴
=
②.
由①,②得:
=
,
∴DM•KE=DN•KF.

∵△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,
∴ID⊥AB,IE⊥BC,
∴∠IDB=∠IEB=90°,
∴∠IDB+∠IEB=180°,
∴I,D,B,E四点共圆.
又∵∠AID=90°-∠IAD,∠MED=∠FDA=90°-∠IAD,
∴∠AID=∠MED,
∴I,D,E,M四点共圆.
∴I,D,B,E,M五点共圆,∠IMB=∠IEB=90°,
即AM⊥BM.
同理,I,D,A,N,F五点共圆,且BN⊥AN.
设直线AN,BM交于点G,则点I为△GAB的垂心.又ID⊥AB,
∴G,I,D共线.
∵G,N,D,B四点共圆,
∴∠ADN=∠G.
同理∠BDM=∠G.
∴DK平分∠MDN,
∴
| DM |
| DN |
| KM |
| KN |
又由I,D,E,M;I,D,N,F分别共圆,
∴KM•KE=KI•KD=KF•KN,
∴
| KM |
| KN |
| KF |
| KE |
由①,②得:
| DM |
| DN |
| KF |
| KE |
∴DM•KE=DN•KF.
看了 如图,△ABC的内切圆I在边...的网友还看了以下:
已知2^a3^b=2^c3^d=6,证明(a-1)(d-1)=(b-1)(c-1)最先证出的给分! 2020-06-06 …
税收的无偿性要求它具有强制性;税收的强制性和无偿性又决定了它必须具有固定性。这说明A.如果纳税人偷 2020-06-26 …
..1个小时内结束...证明.1..如果a大于b..e大于f..c大于0..那么.f-ac小于e- 2020-07-09 …
如图,在△ABC中,BD平分∠ABC,CD平分∠ACE,BD,CD相交于点D,试说明∠A=2∠D. 2020-07-27 …
证明比例关系式(在线等待)例:证明a/b=c/d=(a+b)/(c+d).就象1/2=2/4=(1 2020-07-30 …
如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明 2020-07-30 …
全等三角形问题已知三角形ABC和三角形A'B'C'中,AB=A'B',AC=A'C',如果AD、A 2020-08-01 …
已知非零向量e1和e2不贡献,如果MB=2e1+3e2,BC=6e1+23e2,CD=4e1-8e2 2020-10-31 …
∠DBC=2∠ABD,∠DCB=2∠ACD,试说明∠A与∠D之间的关系 2020-11-03 …
如图所示是原子核的平均结合能与原子序数Z的关系图象,下列说法正确的是()A.如D和E能结合成F,结合 2020-11-17 …