早教吧作业答案频道 -->数学-->
已知F为椭圆x2a2+y2b2=1（a>b>0）的一个焦点，A1、A2为椭圆长轴的两个端点，P为椭圆上任一点，分别以PF、A1A2为直径作圆，则两圆的位置关系为（）A.相交B.相切C.相离D.内含
题目详情
已知F为椭圆
+x2 a2
=1（a>b>0）的一个焦点，A1、A2为椭圆长轴的两个端点，P为椭圆上任一点，分别以PF、A1A2为直径作圆，则两圆的位置关系为（ ）y2 b2
A. 相交
B. 相切
C. 相离
D. 内含
▼优质解答
答案和解析
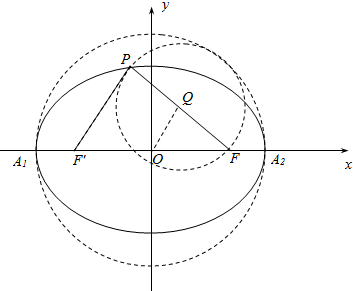记椭圆的另一个焦点为F′，线段PF的中点为Q，
如图，联结OQ、PF′，则OQ为三角形FPF′的中位线，
由椭圆定义可知OQ+QF=
（PF+PF′）=a=OA2，
∴以PF、A1A2为直径所作的两圆相切，
故选：B．
记椭圆的另一个焦点为F′，线段PF的中点为Q，如图，联结OQ、PF′，则OQ为三角形FPF′的中位线，
由椭圆定义可知OQ+QF=
| 1 |
| 2 |
∴以PF、A1A2为直径所作的两圆相切，
故选：B．
看了 已知F为椭圆x2a2+y2b...的网友还看了以下：
一道向量数学题如图给定一个平行四边形ABCD,以CD边为直径作圆P,MN为圆P任意一条直径,问当直 2020-05-16 …
如图所示,AB为半圆的一条直径,O为圆心,P点为圆周上的一点,在P点作用了三个共点力F1、F2、F 2020-05-17 …
心轴为圆柱的螺旋轴叶片如何用CAD2006画展开图 2020-05-17 …
某乡镇准备在相距3千米的A、B两个工厂间修建一条笔直的公路，在工厂A北偏东60°方向，工厂北偏西4 2020-06-15 …
已知P点为圆O1与圆O2公共点，圆O1：（x-a）2+（y-b）2=b2+1，圆O2：（x-c）2 2020-06-30 …
如图所示，Pa，Pb是竖直面内两根固定的光滑细杆，P，a，b，c位于同一圆周上，p点为圆周的最高点 2020-07-20 …
在我市十个全覆盖工作的推动下，某乡镇准备在相距3千米的A、B两个工厂间修一条笔直的公路，在工厂A北 2020-07-22 …
如图，已知∠MON=30°，在ON上有一点P，OP=5cm，若以P点为圆心，r为半径作圆，当射线O 2020-07-24 …
如图，已知抛物线y2=2px（p＞0）上点（2，a）到焦点F的距离为3，直线l：my=x+t（t≠ 2020-07-25 …
（18分）如图所示，一工件置于水平地面上，其AB段为一半径的光滑圆弧轨道，BC段为一长度的粗糙水平 2020-07-31 …