如图所示，竖直平面内固定着有两个半径为R的四分之一圆弧构成的细管道ABC，圆心连线O1O2水平．轻弹簧左端固定在竖直挡板上，右端靠着质量为m的小球（小球的直径略小于管道内径），长

Question

如图所示，竖直平面内固定着有两个半径为R的四分之一圆弧构成的细管道ABC，圆心连线O₁O₂水平．轻弹簧左端固定在竖直挡板上，右端靠着质量为m的小球（小球的直径略小于管道内径），长为R的薄板DE置于水平面上，板的左端D到管道右端C的水平距离为R、开始时弹簧处于锁定状态，具有一定的弹性势能，重力加速度为g，解除锁定，小球离开弹簧后进入管道，最后从C点抛出（不计小球与水平面和细管的摩擦）．

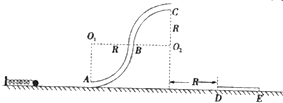
（1）若小球经C点时对轨道外侧的弹力的大小为mg，求弹簧锁定时具有的弹性势能E_p；
（2）试通过计算判断能否落在薄板DE上．

Answer 1

（1）设小球到达C点的速度大小为v₁．
解除弹簧锁定后小球运动到C点过程，弹簧和小球组成的系统机械能守恒，
由机械能守恒定律得：
  E_p=2mgR+(1)/(2)m

v

2 1

；
小球经过C点所受的弹力大小为mg，方向向下．
在C点，由牛顿第二定律得 mg+mg=m(v21)/(R)
解得 E_p=3mgR
（2）小球离开C后做平抛运动，由平抛运动的规律有
  2R=(1)/(2)gt2
  x=v₁t
联立解得 x=2√(2)R
因为x>2R，所以小球不能落在薄板DE上．
答：
（1）弹簧锁定时具有的弹性势能E_p是3mgR．
（2）小球不能落在薄板DE上．