已知定点P(-2，-1)和直线l:(1+3λ)x+(1+2λ)y-(2+5λ)=0(λ∈R).求证：不论λ取何值时，点P到直线l的距离不大于.
求证：不论λ取何值时，点P到直线l的距离不大于 
.
剖析：若直接运用点到直线的距离公式，将P到l的距离d化为关于λ的函数，只需证明该函数的最大值是 .或利用直线系方程，结合图形也可获证.
证法一：由点线距离公式，得
d= 
= 
.
又∵d 2 = 
=13- 
≤13
∴d≤ .
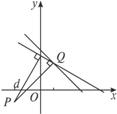
证法二：将原方程化为(x+y-2)+λ(3x+2y-5)=0 显然知l恒过直线x+y-2=0与3x+2y-5=0的交点Q(1 1)，如图，从几何直观可知，只需证明d≤|PQ|.
由|PQ|= 
=
∴原命题得证.
一均匀带电无限长直线外一点处的电场强度大小为E0,该点到带电直线的距离为r,则距离带电直线为r/2 2020-04-13 …
场源电荷Q=2乘10的副4次C是正点电荷检验电荷q=-2乘10的副5次C,是副点电荷他们相距r=2 2020-06-15 …
已知圆C：x²+（y－1）²=5,直线l：mx-y+1-m=0（1）:求证：对任意m∈R,直线l已 2020-07-18 …
若圆（x-3）^2+（y+5）^2=r^2上有且只有两个点到直线4x-3y=2的距离等于1,则半径 2020-07-19 …
△ABC中,∠C=90°,AC=3,AB=6,若以C为圆心,yir为半径作圆,那么:1.当直线AB 2020-07-26 …
物理题求解有一对等量异号的点电荷+q和-q，它们之间的距离为l，在它们连线的延长线上取一点A，A到 2020-07-30 …
已知圆C：x^2+（y-1）^2=5,直线L：mx-y+1-m=0（1）求证：m∈R时,直线L与圆C 2020-11-01 …
满足（z+5)/(z+5i)∈R的复数z对应的曲线为C1,曲线C2：｜z-2(cosπ/6+isin 2020-11-01 …
P和Q是两个同方向，同频率，同相位，同振幅的波源所在处，设他们在介质中产生波的波长为入，PQ之间的距 2020-12-05 …
设数据元素的集合D={1,2,3,4,5}，则满足下列关系R的数据结构中为线性结构的是A)R={(1 2020-12-23 …