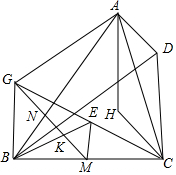
如图，已知H为锐角△ABC的垂心，D是使四边形AHCD为平行四边形的一点，过BC的中点M作AB的垂线，垂足为N，K为MN的中点，过点A作BD的平行线交MN于点G，若A，K，M，C四点共圆．求证：直线BK平分

Question

如图，已知H为锐角△ABC的垂心，D是使四边形AHCD为平行四边形的一点，过BC的中点M作AB的垂线，垂足为N，K为MN的中点，过点A作BD的平行线交MN于点G，若A，K，M，C四点共圆．求证：直线BK平分线段CG．

Answer 1

证明：如图，

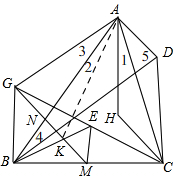
设BK交CG于E，连接AG，AK，
∵A，K，M，C四点共圆，
∴∠ACB=∠AKG（外角等于内对角），
∵H是△ABC的垂心，
∴AH⊥BC，CH⊥AB，
∵四边形AHCD是平行四边形，
∴CH∥AD，AH∥CD，
∴CD⊥BC，AD⊥AB，
∴∠BCD=∠BAD=90°，
∴∠BAD+∠BCD=180°，
∴点A，B，C，D四点共圆，
∴∠5=∠ACB=∠AKG，
∵AH⊥BC，
MN⊥AB，AD⊥AB，
∴∠1=∠2=∠4，
∵AG∥BD，
∴∠3=∠4=∠2，
在△ANG和△ANK中，

∠3=∠2

∠ANG=∠ANK=90°

AN=AN

，
∴△ANG≌△ANK，
∴GN=KN=MK，
∴MK=(1)/(2)KG，
∵直线BKE截得△GMC，
由梅涅劳定理得：(GE)/(EC)•(CB)/(BM)•(MK)/(KG)=1，
∵点M是CB中点，
∴CB=2BM，
∴GE=EC，
∴直线BK平分线段CG．