早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.(1)求证:AM=CN;(2)联结BD,如果BD是AC与MN的比例中项,求证:BE⊥AD.
题目详情
如图,在菱形ABCD中,E、F分别为边AD、CD上的点,且AE=CF,BE和BF交AC于点M、N.
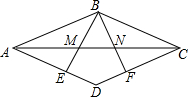
(1)求证:AM=CN;
(2)联结BD,如果BD是AC与MN的比例中项,求证:BE⊥AD.

(1)求证:AM=CN;
(2)联结BD,如果BD是AC与MN的比例中项,求证:BE⊥AD.
▼优质解答
答案和解析
(1)证明:如图1中,
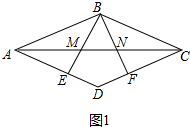
∵四边形ABCD为菱形,
∴AB=BC,∠BAM=∠BCN,∠BAE=∠DAE=∠DCA=∠BCF,
又∵∠AMB=∠CNB=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,
,
∴△ABE≌△CBF(ASA),
∴AE=CF.
(2)如图2中,连接BD交AC于O.
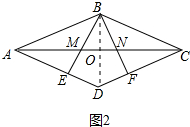
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠BAC=∠DAC,
∵AM=CN(由(1)可知),
∴OM=ON,
∴BD=2OB,AC=2AO,MN=2OM,
∵BD2=MN•AC,
∴4•OB2=2OM•2OA,
∴OB2=OM•OA,
∴
=
,∵∠BOM=∠AOB=90°,
∴△BOM∽△AOB,
∴∠OBM=∠BAO=∠DAC,
∵∠OBM+∠BMO=90°,∠AME=∠OMB,
∴∠EAM+∠AME=90°,
∴∠AEM=90°,即BE⊥AD.

∵四边形ABCD为菱形,
∴AB=BC,∠BAM=∠BCN,∠BAE=∠DAE=∠DCA=∠BCF,
又∵∠AMB=∠CNB=90°,
∴∠ABE=∠CBF,
在△ABE和△CBF中,
|
∴△ABE≌△CBF(ASA),
∴AE=CF.
(2)如图2中,连接BD交AC于O.

∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OB=OD,∠BAC=∠DAC,
∵AM=CN(由(1)可知),
∴OM=ON,
∴BD=2OB,AC=2AO,MN=2OM,
∵BD2=MN•AC,
∴4•OB2=2OM•2OA,
∴OB2=OM•OA,
∴
| OB |
| OM |
| OA |
| OB |
∴△BOM∽△AOB,
∴∠OBM=∠BAO=∠DAC,
∵∠OBM+∠BMO=90°,∠AME=∠OMB,
∴∠EAM+∠AME=90°,
∴∠AEM=90°,即BE⊥AD.
看了 如图,在菱形ABCD中,E、...的网友还看了以下:
一只青蛙在平面直角坐标系上从(1,1)开始,可以按照如下两种方式跳跃1:能从任意一点(a,b)跳到点 2020-03-30 …
已知:f(x)=lg(a^x-b^x)(a>1>b>0)若f(x)在(1,+∞)内恒为正,试比较a 2020-05-13 …
公务员假言命题逻辑:如果A评优了,那么B和C也能评优.为什么是"A→B且C"而不是"A→B或C"公 2020-05-16 …
设长方形的面积是S,相邻两边.设长方形的面积是S,相邻两边分别是a,b,如果S=√96cm^2,b 2020-05-20 …
若a>1,b>2,则a+b>3;这是真命题若a>1,b>2,则a+b“取值范围是”a+b>3;这是 2020-06-03 …
①如果abc<,a,c异号,则b②如果a+b>0,ab<0,则a0,b0,|a||b|?①如果ab 2020-07-09 …
运用等式性质进行的变形,正确的是()A.如果a=b,那么a+c=b-cB.如果a2=3a,那么a= 2020-07-21 …
如果积分的上界是a下界是b那么a,b是开区间(a,b)还是[a,b]?如果a>c>b,上下界分别a 2020-07-31 …
已经知道,设f是[a.b]上的可积函数,若f(x)>=0,x∈[a,b],则定积分∫a^bf(x)d 2020-11-01 …
设a,b为自然数,定义a※b如下:如果a≥b,定义a※b=a-b,如果a<b,则定义a※b=b-a. 2020-11-27 …