早教吧作业答案频道 -->数学-->
如图,已知ABCD是菱形,△EFP的顶点E,F,P分别在线段AB,AD,AC上,且EP=FP.(1)证明:∠EPF+∠BAD=180°;(2)若∠BAD=120°,证明:AE+AF=AP;(3)若∠BAD=θ,AP=a,求AE+AF.
题目详情
如图,已知ABCD是菱形,△EFP的顶点E,F,P分别在线段AB,AD,AC上,且EP=FP.
(1)证明:∠EPF+∠BAD=180°;
(2)若∠BAD=120°,证明:AE+AF=AP;
(3)若∠BAD=θ,AP=a,求AE+AF.
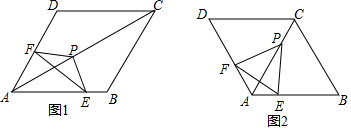
(1)证明:∠EPF+∠BAD=180°;
(2)若∠BAD=120°,证明:AE+AF=AP;
(3)若∠BAD=θ,AP=a,求AE+AF.

▼优质解答
答案和解析
(1)如图1中,作PM⊥AD于M,PN⊥AC于N.
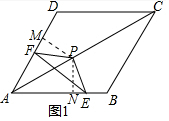
∵四边形ABCD是菱形,
∴∠PAM=∠PAN,
∴PM=PN,
∵PE=PF,
∴Rt△PMF≌Rt△PNE,
∴∠MPF=∠NPE,
∴∠EPF=∠MPF,
∵∠BAD+∠MPN=360°-∠AMP-∠ANP=180°,
∴∠EPF+∠BAD=180°.
(2)如图2中,作PM⊥AD于M,PN⊥AC于N.
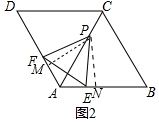
由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN-EN)=2AM,
∵∠BAD=120°,
∴∠PAM=60°,易知PA=2AM,
∴AE+AF=PA.
(3)结论:AF+AE=PA•cos
.
理由:如图2中,作PM⊥AD于M,PN⊥AC于N.
由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN-EN)=2AM,
∵∠BAD=θ,
∴∠PAM=
,易知AM=PA•cos
,
∴AF+AE=PA•cos
.

∵四边形ABCD是菱形,
∴∠PAM=∠PAN,
∴PM=PN,
∵PE=PF,
∴Rt△PMF≌Rt△PNE,
∴∠MPF=∠NPE,
∴∠EPF=∠MPF,
∵∠BAD+∠MPN=360°-∠AMP-∠ANP=180°,
∴∠EPF+∠BAD=180°.
(2)如图2中,作PM⊥AD于M,PN⊥AC于N.

由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN-EN)=2AM,
∵∠BAD=120°,
∴∠PAM=60°,易知PA=2AM,
∴AE+AF=PA.
(3)结论:AF+AE=PA•cos
| θ |
| 2 |
理由:如图2中,作PM⊥AD于M,PN⊥AC于N.
由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN-EN)=2AM,
∵∠BAD=θ,
∴∠PAM=
| θ |
| 2 |
| θ |
| 2 |
∴AF+AE=PA•cos
| θ |
| 2 |
看了 如图,已知ABCD是菱形,△...的网友还看了以下:
导数,不等式结合问题.已知函数F(x)=lnx,G(x)=0.5x^2-2x.(1)设h(x)=F 2020-05-14 …
设f(x)在[a,b]上连续,在(a,b)内可导,且当x∈(a,b)时,f(x)≠0.若f(a)= 2020-05-14 …
设f(x)在闭区间0,1连续,且f(0)=f(1),证必有一点a属于(0,1),使f(a+0.5) 2020-06-22 …
设f(x)在闭区间0,1连续,且f(0)=f(1),证必有一点a属于(0,1),使f(a+0.5) 2020-06-22 …
证明方程x=asinx+b(a>0,b>0)至少有一个正根,并且不超过a+bf(x)在闭区间[0, 2020-07-20 …
若A是n阶矩阵,f(x)是一个常数项不为零的多项式,且满足f(A)=0,证明:A的特征值一定若A是 2020-07-31 …
a>b>0,c=√(1/a(a-b)),求证f(a)+f(c)>4/5√表示根号我又错了不好意思f( 2020-11-01 …
证明题(以下各题中f(x)均是连续函数),1,证明∫(a,b)f(x)dx=(b-a)∫(0,1)f 2020-11-01 …
不可导的充要条件证明若函数f(x)在x=a出可导,则函数|f(x)|在x=a处不可导的充分必要条件是 2020-11-03 …
设f‘’(x)<0,a,b>0,证f(a+b)+f(0)<f(a)+f(b) 2020-11-03 …