早教吧作业答案频道 -->数学-->
如图,菱形ABCD的周长为16,∠DAB=60°,对角线AC上有两点E和F,且AE<12AC,AE=CF.(1)求证:四边形DEBF是菱形;(2)求AC的长.(3)当AE的长为时,四边形DEBF是正方
题目详情
如图,菱形ABCD的周长为16,∠DAB=60°,对角线AC上有两点E和F,且AE<
AC,AE=CF.
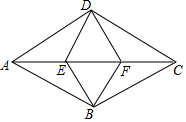
(1)求证:四边形DEBF是菱形;
(2)求AC的长.
(3)当AE的长为___时,四边形DEBF是正方形(不必证明).
| 1 |
| 2 |

(1)求证:四边形DEBF是菱形;
(2)求AC的长.
(3)当AE的长为___时,四边形DEBF是正方形(不必证明).
▼优质解答
答案和解析
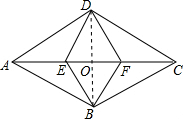 (1)证明:连接BD,交AC于O,如图所示:
(1)证明:连接BD,交AC于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2) 在菱形ABCD中,菱形ABCD的周长为16,∠DAB=60°,
则AD=4,∠DAO=30°,AC⊥BD且AC=2OA,
在直角△AOD中,OA=AD•cos30°=4×
=2
,
故AC=2OA=4
;
(3) 当AE=2
-2时,四边形DEBF是正方形.理由如下:
由(1)知,四边形DEBF是菱形.
当OD=OE时,四边形DEBF是正方形.
∵在直角△AOD中,∠DAO=30°,AD=4,
∴OD=
AD=2,OA=2
,
∴AE=OA-OD=2
-2.
故答案是:2
-2.
 (1)证明:连接BD,交AC于O,如图所示:
(1)证明:连接BD,交AC于O,如图所示:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2) 在菱形ABCD中,菱形ABCD的周长为16,∠DAB=60°,
则AD=4,∠DAO=30°,AC⊥BD且AC=2OA,
在直角△AOD中,OA=AD•cos30°=4×
| ||
| 2 |
| 3 |
故AC=2OA=4
| 3 |
(3) 当AE=2
| 3 |
由(1)知,四边形DEBF是菱形.
当OD=OE时,四边形DEBF是正方形.
∵在直角△AOD中,∠DAO=30°,AD=4,
∴OD=
| 1 |
| 2 |
| 3 |
∴AE=OA-OD=2
| 3 |
故答案是:2
| 3 |
看了 如图,菱形ABCD的周长为1...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
勾股定理的适用范围:钝角三角形三边长a,b.c.且c边最长,则.锐角三角形三边长为a,b,c,且c 2020-06-10 …
((a,(b,c)),a,(b,c))与((a,(b,c)),(a,(b,c)))的表头和表尾是相 2020-07-16 …
设a.b.c.都是正数,且有a^2+b^2-c^2+2ab=0,那么分别以a.b.c为长度的三条设 2020-07-30 …
1.如果直角三角形的直角边长为8,15,则斜边边长为———,斜边长为————.2.如果三角形ABC 2020-08-02 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
在ABC中,a.b.c分别为角A角B角C的对边长,已知(2bc)cos...在ABC中,a.b.c分 2020-11-24 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
三角形内,acosB=3,bsinA=4,求边长a,设三角形ABC的内角A,B,C所对的边长分别为a 2020-12-25 …
(1)已知三角形ABC中2B=A+C,且边长b=3,c=2求边长a.(2)ABC面积为16(1)已知 2021-02-07 …