如图，菱形ABCD中，∠BAD=60°，AC与BD交于点O，E为CD延长线上的一点，且CD=DE，连结BE，分别交AC，AD于点F、G，连结OG，则下列结论：①OG=12AB；②图中与△EGD全等的三角形共有5个；③由点A、B、D

Question

如图，菱形ABCD中，∠BAD=60°，AC与BD交于点O，E为CD延长线上的一点，且CD=DE，连结BE，分别交AC，AD于点F、G，连结OG，则下列结论：
①OG=

(1)/(2)AB；
②图中与△EGD全等的三角形共有5个；
③由点A、B、D、E构成的四边形是菱形；
④S_{四边形ODGF}=S_△ABF，其中正确的结论是（　　）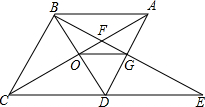

A. ①③

B. ①③④

C. ①②③

D. ②③④

Answer 1

∵四边形ABCD是菱形，
∴AB=BC=CD=DA，AB∥CD，OA=OC，OB=OD，AC⊥BD，
∴∠BAG=∠EDG，△ABO≌△BCO≌△CDO≌△AOD，
∵CD=DE，
∴AB=DE，
在△ABG和△DEG中，

∠BAG=∠EDG

∠AGB=∠DGE

AB=DE

，
∴△ABG≌△DEG（AAS），
∴AG=DG，
∴OG是△ACD的中位线，
∴OG=(1)/(2)CD=(1)/(2)AB，
∴①正确；
∵AB∥CE，AB=DE，
∴四边形ABDE是平行四边形，
∵∠BCD=∠BAD=60°，
∴△ABD、△BCD是等边三角形，
∴AB=BD=AD，∠ODC=60°，
∴OD=AG，四边形ABDE是菱形，
④正确；
∴AD⊥BE，
由菱形的性质得：△ABG≌△BDG≌△DEG，
在△ABG和△DCO中，

OD=AG

∠ODC=∠BAG=60°

AB=DC

，
∴△ABG≌△DCO（SAS），
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG，
∴②不正确；
∵OB=OD，AG=DG，
∴OG是△ABD的中位线，
∴OG∥AB，OG=(1)/(2)AB，
∴△GOD∽△ABD，△ABF∽△OGF，
∴△GOD的面积=(1)/(4)△ABD的面积，△ABF的面积=△OGF的面积的4倍，AF：OF=2：1，
∴△AFG的面积=△OGF的面积的2倍，
又∵△GOD的面积=△AOG的面积=△BOG的面积，
∴S_{四边形ODGF}=S_△ABF；
③正确；
正确的是①③④．
故选B．