早教吧作业答案频道 -->数学-->
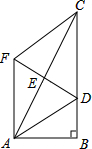
如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.
题目详情
如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
求证:四边形ADCF是菱形.

▼优质解答
答案和解析
证明:∵AF∥CD,
∴∠AFE=∠CDE,
在△AFE和△CDE中,
,
∴△AEF≌△CED.
AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形.
由题意知,AE=AB,∠EAD=∠BAD,AD=AD,
∴△AED≌△ABD.
∴∠AED=∠B=90°,即DF⊥AC.
∴四边形ADCF是菱形.
∴∠AFE=∠CDE,
在△AFE和△CDE中,
|
∴△AEF≌△CED.
AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形.
由题意知,AE=AB,∠EAD=∠BAD,AD=AD,
∴△AED≌△ABD.
∴∠AED=∠B=90°,即DF⊥AC.
∴四边形ADCF是菱形.
看了 如图,在Rt△ABC中,∠B...的网友还看了以下:
先作半径为22的圆的内接正方形,接着作上述内接正方形的内切圆,再作上述内切圆的内接正方形,…,则按 2020-04-25 …
如图是一个正方形,A和B分别是等腰直角三角形的两种不同的内接正方形,那么正方形A和正方形B的面积比 2020-06-05 …
如图,已知一个正方形内接于另一个固定的正方形,问;a取什么值时,内接正方形面积最小?用导数的方法, 2020-06-16 …
有关“接近度”的数学问题设矩形相邻两条边长分别为a和b(a小于等于b),将矩形的“接近度”定义为a 2020-06-19 …
问9^9-9^2最接近哪个数,A.9^10B.9^9C.9^8D.9^7 2020-06-23 …
(满分9分)如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,D 2020-08-02 …
如图,已知三角形ABC内接于一圆,角A=57度,角B=66度,过点A、B、C作该圆的外切三角形A' 2020-08-03 …
那道果蝇题您已经解答过了,但是我有个疑问,已经推出黑身aa的果蝇概率为1\9,直接用1-1\9可得出 2020-11-27 …
如图所示,三相交流发电机的三个线圈和三相负载的接法中,正确的说法有()A.都为星形连接B.都为三角形 2020-12-25 …
如图4-1-9所示,三相交流发电机的三个线圈和三相负载的接法中,正确的说法有()图4-1-9A.都为 2020-12-25 …