早教吧作业答案频道 -->数学-->
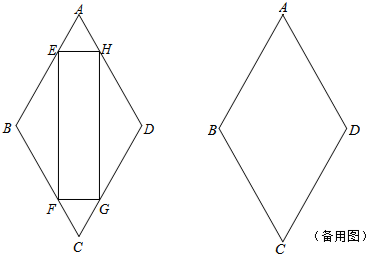
(1)已知:如图,E、F、G、H分别是菱形ABCD的各边上与顶点均不重合的点,且AE=CF=CG=AH.求证:四边形EFGH是矩形.(2)已知:E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD上与顶点均不重合的
题目详情
(1)已知:如图,E、F、G、H分别是菱形ABCD的各边上与顶点均不重合的点,且AE=CF=CG=AH.
求证:四边形EFGH是矩形.
(2)已知:E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD上与顶点均不重合的点,且四边形EFGH是矩形.AE与AH相等吗?如果相等,请说明理由;如果不相等,请举反例进行说明.
求证:四边形EFGH是矩形.
(2)已知:E、F、G、H分别是菱形ABCD的边AB、BC、CD、AD上与顶点均不重合的点,且四边形EFGH是矩形.AE与AH相等吗?如果相等,请说明理由;如果不相等,请举反例进行说明.

▼优质解答
答案和解析
(1) 证明:∵四边形ABCD是菱形,
证明:∵四边形ABCD是菱形,
∴∠A=∠C,∠B=∠D,AB=BC=CD=DA
∵AE=AH=CF=CG,
∴BE=BF=DH=DG,
在△AEH与△CGF中,
.
∴△AEH≌△CGF,
同理△BEF≌△DGH,
∴EH=FG,EF=GH,
∴四边形EFGH是平行四边形,
∵∠A+∠D=180°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形EFGH是矩形;
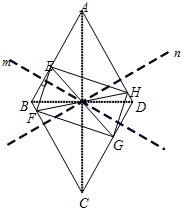
(2)如图,m、n是经过菱形对角线交点且与对边垂直的2条直线,交AB于P,交AD于Q,
由(1)知,△AEH≌△CGF,△BEF≌△DGH,显然,AE与AH不相等.
故AE和AH不一定相等.
 证明:∵四边形ABCD是菱形,
证明:∵四边形ABCD是菱形,∴∠A=∠C,∠B=∠D,AB=BC=CD=DA
∵AE=AH=CF=CG,
∴BE=BF=DH=DG,
在△AEH与△CGF中,
|
∴△AEH≌△CGF,
同理△BEF≌△DGH,
∴EH=FG,EF=GH,
∴四边形EFGH是平行四边形,
∵∠A+∠D=180°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形EFGH是矩形;
(2)如图,m、n是经过菱形对角线交点且与对边垂直的2条直线,交AB于P,交AD于Q,
由(1)知,△AEH≌△CGF,△BEF≌△DGH,显然,AE与AH不相等.
故AE和AH不一定相等.
看了 (1)已知:如图,E、F、G...的网友还看了以下:
有关概率论 相互独立的随机变量书上是怎么由相互独立情况下F(X,Y)=F(X)F(Y) 得出f(X 2020-04-06 …
三角形函数若a,b,c是任意一个三角形的三边长,函数f(x)满足若a,b,c均是函数f(x)定义域 2020-06-02 …
设函数f(x)=sin2x+2√3cosx+3-√3求(1)求f(x)的最小正周期:(2)在ABC 2020-06-06 …
急(空间几何)!空间四边形ABCD的边长及对角线AD,BC的长均为a,E,F分别是BC与AD的中点 2020-06-18 …
已知A、B是直线y=0与函数f(x)=2cos^2wx/2+cos(wx+派/3)-1(w>0)图 2020-07-30 …
已知f(x)=cosx-cos(x+π/3)一、求函数f(x)在区间R上的最小直和最大值二、在三角 2020-08-02 …
F=A+A×(1+i)+…+A×(1+i)n-1,(1)等式两边同乘以(1+i):F(1+i)=A( 2020-11-01 …
已知函数f(x)=log(2)X(2是底数,X为真数),对于任意a,b,c属于[M,+无穷),且a≧ 2020-11-06 …
已知f(x)=(x^+kx+1)/x^+x+1若对任何实数abc,f(a),f(b),f(c)均为三 2020-11-12 …
已知函数f(x),若对给定的△ABC,它的三边的长a,b,c均在函数f(x)的定义域内,都有f(a) 2020-11-20 …