早教吧作业答案频道 -->数学-->
分别以平行四边形ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形:△ABE、△CDG,△ADF.(1)如图①,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF
题目详情
分别以平行四边形ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形:△ABE、△CDG,△ADF.
(1)如图①,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系,并进行证明.
(2)如图②,当三个等腰直角三角形都在该平行四边形内部时,连接EF,EF,(1)中的结论还成立吗?若成立,给出证明;若不成立,说明理由.
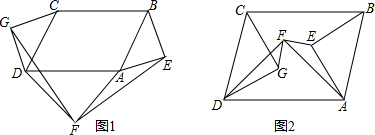
(1)如图①,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系,并进行证明.
(2)如图②,当三个等腰直角三角形都在该平行四边形内部时,连接EF,EF,(1)中的结论还成立吗?若成立,给出证明;若不成立,说明理由.

▼优质解答
答案和解析
(1)GF⊥EF,GF=EF.理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA,
∠EAF=360°-∠BAE-∠DAF-∠BAD=270°-(180°-∠CDA)=90°+∠CDA,
∴∠FDG=∠EAF,
∵在△EAF和△GDF中,
,
∴△EAF≌△GDF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF,GF=EF;
(2)GF⊥EF,GF=EF成立;
理由:∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠BAE+∠DAF+∠EAF+∠ADF+∠FDC=180°,
∴∠EAF+∠CDF=45°,
∵∠CDF+∠GDF=45°,
∴∠FDG=∠EAF,
∵在△GDF和△EAF中,
,
∴△GDF≌△EAF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF,GF=EF.
∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA,
∠EAF=360°-∠BAE-∠DAF-∠BAD=270°-(180°-∠CDA)=90°+∠CDA,
∴∠FDG=∠EAF,
∵在△EAF和△GDF中,
|
∴△EAF≌△GDF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF,GF=EF;
(2)GF⊥EF,GF=EF成立;
理由:∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠BAE+∠DAF+∠EAF+∠ADF+∠FDC=180°,
∴∠EAF+∠CDF=45°,
∵∠CDF+∠GDF=45°,
∴∠FDG=∠EAF,
∵在△GDF和△EAF中,
|
∴△GDF≌△EAF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF,GF=EF.
看了 分别以平行四边形ABCD(∠...的网友还看了以下:
如何判断浮力公式的使用浮力公式一共大概五个:1.F浮=G物2.F浮=F向上—F向下3.F浮=G-F 2020-05-16 …
在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、 2020-06-18 …
某超市员工将各品牌洗发液摆上货架,已知洗发液有E、F、G、H、I等五个品牌,在货架上从左向右排列, 2020-07-12 …
1.已知f(x)是定义在R上的函数,设g(x)=[f(x)+f(-x)]/2,h(x)=[f(x) 2020-07-19 …
高等数学:设函数f(x)和g(x)在(-无穷,+无穷)内有定义,f(x)为连续函数,且f(x)≠0 2020-07-21 …
导数乘法证明中h是什么意思?(f(x)g(x))'=lim(h→0)[f(x+h)g(x+h)-f 2020-07-22 …
高数间断点问题设f(x)在R上连续,且f(x)不等于0,g(x)在R上有定义,且有间断点,则下列陈 2020-07-30 …
数分中的函数连续性问题f是R上的单调函数,g(x)=f(x+0),证明g在R上处处单调.我自己在做 2020-08-02 …
(1)如图1,四边形ABCD是矩形,E为AD上一点,且BE=ED,P为对角线BD上一点,PF⊥BE于 2020-11-03 …
如图所示,以O为支点,杠杆(自重不计)在力F和重力G的作用下,在水平位置处于平衡状态,下列判断中正确 2020-12-17 …