早教吧作业答案频道 -->数学-->
如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.(1)求证:△ADF∽△BAG;(2)若DF=4,请连接EF并求出EF的长.
题目详情
如图,矩形ABCD中,AD=5,AB=10,分别以AD、BC为斜边向矩形外作Rt△ADF≌Rt△CBE,延长FA、EB交于点G.
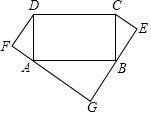
(1)求证:△ADF∽△BAG;
(2)若DF=4,请连接EF并求出EF的长.

(1)求证:△ADF∽△BAG;
(2)若DF=4,请连接EF并求出EF的长.
▼优质解答
答案和解析
(1)∵四边形ABCD为矩形,
∴∠DAB=90°,即∠DAF+∠BAG=90°,
又∵∠DAF+∠ADF=90°,
∴∠ADF=∠BAG,
同理∠ECB=∠GBA,
∵△ADF≌△CBE,
∴∠ECB=∠DAF,
∴∠DAF=∠GBA,
∵在△ADF和△BAG中,
,
∴△ADF∽△BAG;
(2)连接EF,如图,
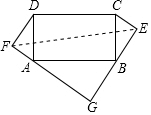
∵在Rt△ADF中,AD=5,DF=4,∴AF=
=3,
∵△ADF∽△BAG,
∴
=
=
,∠AGB=∠AFD=90°,
∴AG=8,BG=6,
∴FG=AF+AG=11,EG=EB+BG=DF+BG=4+6=10,
∴在Rt△EFG中,EF=
=
.
∴∠DAB=90°,即∠DAF+∠BAG=90°,
又∵∠DAF+∠ADF=90°,
∴∠ADF=∠BAG,
同理∠ECB=∠GBA,
∵△ADF≌△CBE,
∴∠ECB=∠DAF,
∴∠DAF=∠GBA,
∵在△ADF和△BAG中,
|
∴△ADF∽△BAG;
(2)连接EF,如图,

∵在Rt△ADF中,AD=5,DF=4,∴AF=
| AD2-DF2 |
∵△ADF∽△BAG,
∴
| AD |
| AB |
| DF |
| AG |
| AF |
| GB |
∴AG=8,BG=6,
∴FG=AF+AG=11,EG=EB+BG=DF+BG=4+6=10,
∴在Rt△EFG中,EF=
| FG2+EG2 |
| 221 |
看了 如图,矩形ABCD中,AD=...的网友还看了以下:
设函数f(x)(x属于R)为奇函数,f(1)=1/2,f(x+2)=f(x)+f(2)求f(5)的 2020-04-27 …
1.已知(x-1)^5=ax^5+bx^4+cx^3+dx^2;+ex+f.(^5表示五次方,^4 2020-05-16 …
设f(x)=ax五次方+bx三次方+x平方-1(a,b为常数),若f(-5)=2,则f(5)= 2020-05-21 …
设f(x)=1/[(2^x)+√2],则f(-5)+f(-4)+f(-3)+…+f(0)+f(1) 2020-05-23 …
已知f(x)=x^5-ax^3+bsinx+2且f(-5)=17,则f(5)的值为? 2020-05-24 …
设函数f(x)(x属于R)为奇函数,f[1]=1/2,f[x+2]=f[x]+f[2],则f[5] 2020-06-05 …
设函数f(x)(x∈R)为奇函数,已知f(1)=1/2,f(x+2)=f(x)+f(2),则f(5 2020-06-06 …
已知f(x)对一切x,y都有f(x+y)=f(x)+f(y).求证(1)f(x)是奇函数(2)若f 2020-06-07 …
已知f(x)=1/(2^x+根号2),求f(-5)+f(-4)+.f(0)+.f(6) 2020-06-12 …
已知f(x)是奇函数,且有f(x+1)=-1/f(x),当x∈(0,1/2)时,f(x)=8^x(1 2020-11-07 …