早教吧作业答案频道 -->数学-->
如图,点A(0,a),B(b,0)分别在y轴正半轴、x轴正半轴上,C为AB的中点,a,b满足a2-2ab+b2=-|b-4|.(1)写出A,B两点坐标,并判断△AOB的形状;(2)若一直角三角板直角顶点与C重合,两
题目详情
如图,点A(0,a),B(b,0)分别在y轴正半轴、x轴正半轴上,C为AB的中点,a,b满足a2-2ab+b2=-|b-4|.
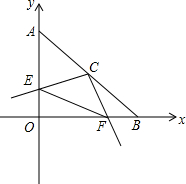
(1)写出A,B两点坐标,并判断△AOB的形状;
(2)若一直角三角板直角顶点与C重合,两边分别交OA,OB交于E,F两点,求OE+OF的值.

(1)写出A,B两点坐标,并判断△AOB的形状;
(2)若一直角三角板直角顶点与C重合,两边分别交OA,OB交于E,F两点,求OE+OF的值.
▼优质解答
答案和解析
 (1)∵a2-2ab+b2=-|b-4|,
(1)∵a2-2ab+b2=-|b-4|,
∴(a-b)2+|b-4|=0,
∴a=b=4,
∴A,B两点坐标A(0,4),B(4,),
∴OA=OB=4,
∵AO⊥BO,
∴△AOB是等腰直角三角形;
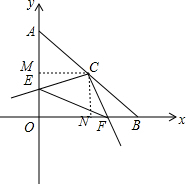
(2)作MC⊥y轴于M,作NC⊥x轴于N,如图所示:
∵C为AB的中点,
则MC=CN=
BC=2,四边形OMCN是正方形,∠EMC=∠CNF=90°,
∴OM=ON=MC=CN=2,∠MCN=90°,
∵∠ECF=90°,
∴∠MCE=∠FCN,
在△MCE和△NCF中,
,
∴△MCE≌△NCF,
∴ME=NF,
∴OE+OF=OM-ME+ON+NF=OM+ON=2+2=4.
 (1)∵a2-2ab+b2=-|b-4|,
(1)∵a2-2ab+b2=-|b-4|,∴(a-b)2+|b-4|=0,
∴a=b=4,
∴A,B两点坐标A(0,4),B(4,),
∴OA=OB=4,
∵AO⊥BO,
∴△AOB是等腰直角三角形;
(2)作MC⊥y轴于M,作NC⊥x轴于N,如图所示:
∵C为AB的中点,
则MC=CN=
| 1 |
| 2 |
∴OM=ON=MC=CN=2,∠MCN=90°,
∵∠ECF=90°,
∴∠MCE=∠FCN,
在△MCE和△NCF中,
|
∴△MCE≌△NCF,
∴ME=NF,
∴OE+OF=OM-ME+ON+NF=OM+ON=2+2=4.
看了 如图,点A(0,a),B(b...的网友还看了以下:
根据图中的A、B两图,回答下列问题:(1)分别判断A、B两图所示的细胞的类型:A图所示的细胞是细胞 2020-05-02 …
△ABC的三边长分别是a、b、c且根号a-1=根号b-2=0,若c为整数,试判断△ABC的形状错了 2020-05-13 …
一个正方体6个面风别写A、B、C、D、E、F,根据下面摆放的3种情况,判断每个字母对面的字母是什么 2020-05-16 …
已知△ABC的三条边长分别为a、b、c,且满足关系:(a+b)2+c2=3ab+c(a+b),试判 2020-07-09 …
已知曲线C的方程为:ax2+ay2-2a2x-4y=0(a≠0,a为常数).(1)判断曲线C的形状 2020-07-10 …
请给出我ABC分别应该判几年,并给出详细的计算过程,谢谢法律人士请进A.甲犯A、B罪,分别被判处有 2020-07-10 …
△ABC中,∠A、∠B、∠C的对边分别为a、b、c,且满足a^2+b^2+c^2-ab-ac-bc 2020-07-22 …
在△ABC中,A.B.C的对边分别是a,b,c,且sinA/a=cosB/b=cosC/c,试判断 2020-07-27 …
在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,根据下列各边的长度,判断各三角形是否是=在△ 2020-07-30 …
设函数f(x)=根号!x加1!x减2!减a,注:f(x)等号后面是共一个根号的,a-b!就是绝对值a 2020-12-31 …