早教吧作业答案频道 -->数学-->
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.(1)求证:A1C⊥平面C1EB;(2)求直线CC1与平面ABC所成角的余弦值.
题目详情
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.
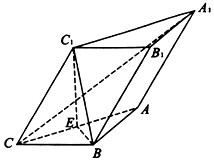
(1)求证:A1C⊥平面C1EB;
(2)求直线CC1与平面ABC所成角的余弦值.

(1)求证:A1C⊥平面C1EB;
(2)求直线CC1与平面ABC所成角的余弦值.
▼优质解答
答案和解析
(1)证明:∵AB=BC,E为AC的中点,∴BE⊥AC,
∵平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC=AC,
∴BE⊥平面A1ACC1,
∵A1C⊂平面A1ACC1,∴BE⊥A1C.
又BC1⊥A1C,BE∩BC1=B,∴A1C⊥面C1EB.
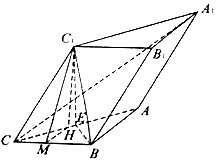
(2) ∵面A1ACC1⊥面ABC,∴C1在面ABC上的射影H在AC上,
∴∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,
在Rt△C1CM中,CM=CC1cos∠C1CM=2cos60°=1.
在Rt△CMH中,CH=
=
.
∴在Rt△C1CH中,cos∠C1CH=
=
=
.
∴直线C1C与面ABC所成的角的余弦值为
∵平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC=AC,
∴BE⊥平面A1ACC1,
∵A1C⊂平面A1ACC1,∴BE⊥A1C.
又BC1⊥A1C,BE∩BC1=B,∴A1C⊥面C1EB.
(2) ∵面A1ACC1⊥面ABC,∴C1在面ABC上的射影H在AC上,
∴∠C1CA为直线C1C与面ABC所成的角.过H作HM⊥BC于M,连C1M,
在Rt△C1CM中,CM=CC1cos∠C1CM=2cos60°=1.
在Rt△CMH中,CH=
| CM |
| cos∠ACB |
2
| ||
| 3 |
∴在Rt△C1CH中,cos∠C1CH=
| CH |
| CC1 |
| ||||
| 2 |
| ||
| 3 |
∴直线C1C与面ABC所成的角的余弦值为
| ||
| 3 |

看了 如图,在三棱柱ABC-A1B...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
能判定△ABC与△A'B'C'相似的条件是( )A.A'B'分之AB=A'C'分之AC B. 2020-05-16 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
求教分析一道代数式值题的解答过程.题目是这样的:已知(b+c)/a=(a+c)/b=(a+b)/c 2020-05-20 …
有难度M{A,B,C}==(A+B+C)/3m{A,B,C}=A(A为三数中最小的一个)则若M{A 2020-06-13 …
a(b-c)^5+b(c-a)^5+c(a-b)^5分解为(a-b)(b-c)(c-a)L(aa( 2020-07-09 …
求证:A∩(B∪C)=(A∪B)∩(A∪C)(1)假设x∈A∩(B∪C),则x∈A且x∈B∪C,所 2020-07-20 …
设a,b,c都是正数且a+b+c=1,求证:(1+a)(1+b)(1+c)≥8(1-a)(1-b) 2020-07-25 …
有三个数a,b,c,其中满足a+b>c,b+c>a,a+c>b,结果是有三个数a,b,c,其中满足a 2020-11-01 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …