早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,O为原点,点A(2,0),点C(0,4),矩形OABC的对角线的交点为M,点P(2,3).(1)直线OB的解析式为;(2)过点P且与直线OB平行的直线的解析式为;(3
题目详情
如图,在平面直角坐标系中,O为原点,点A(2,0),点C(0,4),矩形OABC的对角线的交点为M,点P(2,3).
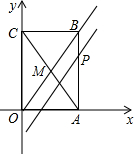
(1)直线OB的解析式为___;
(2)过点P且与直线OB平行的直线的解析式为___;
(3)点M的坐标为___;
(4)点Q在直线AC上,△QMB的面积与△PMB的面积相等,求点Q的坐标.

(1)直线OB的解析式为___;
(2)过点P且与直线OB平行的直线的解析式为___;
(3)点M的坐标为___;
(4)点Q在直线AC上,△QMB的面积与△PMB的面积相等,求点Q的坐标.
▼优质解答
答案和解析
(1)∵四边形OABC是矩形,点A(2,0),点C(0,4),
∴B(2,4).
设直线OB的解析式为为y=kx,
则2k=4,解得k=2,
∴直线OB的解析式为为y=2x.
故答案为y=2x;
(2)设过点P且与直线OB平行的直线的解析式为y=2x+b,
将P(2,3)代入,
得4+b=3,解得b=-1,
所以过点P且与直线OB平行的直线的解析式为y=2x-1.
故答案为y=2x-1;
(3)∵矩形OABC的对角线的交点为M,
∴M是线段AC的中点,
∵点A(2,0),点C(0,4),
∴M(1,2).
故答案为(1,2);
(4)∵点Q在直线AC上,△QMB的面积与△PMB的面积相等,
∴Q到BM的距离等于P到BM的距离.
①如果Q在BM的下方,那么PQ∥BM,Q为直线AC与直线y=2x-1的交点.
∵点A(2,0),点C(0,4),
∴直线AC的解析式为y=-2x+4.
由
,解得
,
∴点Q1的坐标为(
,
);
②如果Q在BM的上方,那么Q与(
,
)关于点M对称,
∵M(1,2),
∴点Q2的坐标为(1×2-
,2×2-
),即(
,
);
故所求点Q的坐标为(
,
)或(
,
).
∴B(2,4).
设直线OB的解析式为为y=kx,
则2k=4,解得k=2,
∴直线OB的解析式为为y=2x.
故答案为y=2x;
(2)设过点P且与直线OB平行的直线的解析式为y=2x+b,
将P(2,3)代入,
得4+b=3,解得b=-1,
所以过点P且与直线OB平行的直线的解析式为y=2x-1.
故答案为y=2x-1;
(3)∵矩形OABC的对角线的交点为M,
∴M是线段AC的中点,
∵点A(2,0),点C(0,4),
∴M(1,2).
故答案为(1,2);
(4)∵点Q在直线AC上,△QMB的面积与△PMB的面积相等,
∴Q到BM的距离等于P到BM的距离.
①如果Q在BM的下方,那么PQ∥BM,Q为直线AC与直线y=2x-1的交点.
∵点A(2,0),点C(0,4),
∴直线AC的解析式为y=-2x+4.
由
|
|
∴点Q1的坐标为(
| 5 |
| 4 |
| 3 |
| 2 |
②如果Q在BM的上方,那么Q与(
| 5 |
| 4 |
| 3 |
| 2 |
∵M(1,2),
∴点Q2的坐标为(1×2-
| 5 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 5 |
| 2 |
故所求点Q的坐标为(
| 5 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 5 |
| 2 |
看了 如图,在平面直角坐标系中,O...的网友还看了以下:
已知平行四边行对角两顶点坐标,求令两对角顶点坐标那已知长方形长跟宽,和两对角顶点坐标,如何求令两对 2020-05-13 …
如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C 2020-06-14 …
如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(4,4)处,两直角边与坐标轴交于点A和点 2020-07-10 …
在方格纸上有A,B两点,若以点B为原点建立直角坐标系,则点A的坐标为(3,4).若以A点为原点建立 2020-07-15 …
(2009•怀柔区一模)如图1,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以 2020-07-21 …
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限 2020-07-30 …
如图,正方形ABCD在平面直角坐标系中的位置如图所示,点B与原点重合,点D的坐标为(4,4),当三 2020-08-02 …
如图,在平面直角坐标系中,A点坐标是(2,0),B点坐标是(0,-2),点P是x轴上运动的点.(1 2020-08-02 …
如图,在平面直角坐标系中,将一块腰长为5的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角 2020-12-25 …
如图,在直角坐标系中,将△AOB连续作旋转变换,依次得到三角形①②③④…,则三角形⑩的直角顶点坐标为 2020-12-25 …