早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为.
题目详情
如图,在平面直角坐标系中,A,B两点的坐标分别为(-4,0),(0,3),连接AB.点P在第二象限,若以点P,A,B为顶点的三角形是等腰直角三角形,则点P坐标为___.

▼优质解答
答案和解析
 分三种情况讨论:
分三种情况讨论:
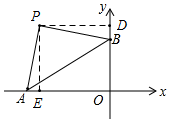
①如图所示,当∠APB=90°时,过P作PE⊥x轴,过P作PD⊥y轴,则∠PEA=∠PDB=90°,
∵∠AOB=90°,
∴∠DPE=90°,
又∵∠APD=90°,
∴∠APE=∠BDP,
在△APE和△BDP中,
,
∴△APE≌△BDP(AAS),
∴PD=PE=OE=OD,AE=BD,
设PD=PE=OE=OD=a,
又∵A,B两点的坐标分别为(-4,0),(0,3),
∴AO=4,BO=3,
∵AO-OE=OD+BO,
即4-a=a-3,
解得a=
,
∴P(-
,
);
②如图所示,当∠ABP=90°时,过点P作PD⊥y轴于点D,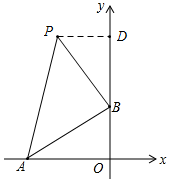
∴∠AOB=∠BDP,∠BPD+∠PBD=90°,∠ABO+∠PBD=90°,
∴∠ABO=∠BPD,
在△ABO和△BPD中,
,
∴△ABO≌△BPD(AAS),
∴PD=BO=3,BD=AO=4,
则OD=BO+BD=7,
∴P(-3,7);
③如图所示,当∠BAP=90°时,过P作PD⊥x轴于D,
∵∠ABO+∠OAB=90°,∠PAD+∠OAB=90°,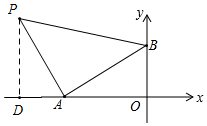
∴∠ABO=∠PAD,
在△ABO和△PAD中,
,
∴△ABO≌△PAD(AAS),
∴AD=OB=3,PD=OA=4,
∴OD=OA+OB=4+3=7,
∴P的坐标为(-7,4);
综上所述,点P坐标为(-
,
)或(-3,7)或(-7,4).
故答案为:(-
,
)或(-3,7)或(-7,4).
 分三种情况讨论:
分三种情况讨论:①如图所示,当∠APB=90°时,过P作PE⊥x轴,过P作PD⊥y轴,则∠PEA=∠PDB=90°,
∵∠AOB=90°,
∴∠DPE=90°,
又∵∠APD=90°,
∴∠APE=∠BDP,
在△APE和△BDP中,
|
∴△APE≌△BDP(AAS),
∴PD=PE=OE=OD,AE=BD,
设PD=PE=OE=OD=a,
又∵A,B两点的坐标分别为(-4,0),(0,3),
∴AO=4,BO=3,
∵AO-OE=OD+BO,
即4-a=a-3,
解得a=
| 7 |
| 2 |
∴P(-
| 7 |
| 2 |
| 7 |
| 2 |
②如图所示,当∠ABP=90°时,过点P作PD⊥y轴于点D,

∴∠AOB=∠BDP,∠BPD+∠PBD=90°,∠ABO+∠PBD=90°,
∴∠ABO=∠BPD,
在△ABO和△BPD中,
|
∴△ABO≌△BPD(AAS),
∴PD=BO=3,BD=AO=4,
则OD=BO+BD=7,
∴P(-3,7);
③如图所示,当∠BAP=90°时,过P作PD⊥x轴于D,
∵∠ABO+∠OAB=90°,∠PAD+∠OAB=90°,

∴∠ABO=∠PAD,
在△ABO和△PAD中,
|
∴△ABO≌△PAD(AAS),
∴AD=OB=3,PD=OA=4,
∴OD=OA+OB=4+3=7,
∴P的坐标为(-7,4);
综上所述,点P坐标为(-
| 7 |
| 2 |
| 7 |
| 2 |
故答案为:(-
| 7 |
| 2 |
| 7 |
| 2 |
看了 如图,在平面直角坐标系中,A...的网友还看了以下:
在六边形的顶点处分别标上1 2 3 4 5 6能否使其任意三个顶点的和大于9,若能,怎么标,若不能 2020-05-13 …
把边长为4的等边三角形ABC置于直角坐标系中,使得顶点B在原点,顶点C在x轴上,若点C把边长为4的 2020-05-16 …
已知二次函数y=ax平方+(b-1)x-2的图象经过点A(-3,-2)B(1,-6)求抛物线解析式 2020-05-16 …
1、若点M(五分之3m-2,三分之m+1)在y轴上,则m=,此时点M的坐标是.2、点P(x,y)1 2020-06-14 …
已知点A(4,0)和圆B:x^2+(y-2)^2=1,若点P在圆B上运动,O是坐标原点,求使S三角 2020-06-14 …
已知抛物线y=x2-4x-121)求抛物线与x轴交点A,B的坐标2)若抛物线顶点为P,求三角形PA 2020-06-14 …
平面直角坐标系中,直线L1:Y=-二分之一X+6分别与X轴、Y轴交于点B、C,且与L2:Y=二分之 2020-06-27 …
数学平面直角系坐标若点P(a-1,a+1)到X轴距离是3且位于第一象限,求它到y轴的距离速度要!过 2020-08-01 …
如图直线Y=3/4Xy轴分别交于点EF两点,点A的坐标为(-6,0),点P在直线EF上运动求E和F两 2020-12-25 …
在平面直角坐标系中,点A的坐标为(2,-2),点B的坐标为(4,2)(1)若点C在y轴上,且AC=B 2020-12-25 …