设在区间上有定义若都有则称是区间的向上凸函数;若都有则称是区间的向下凸函数.有下列四个判断:①若是区间的向上凸函数,则是区间的向下凸函数;
设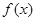 在区间
在区间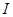 上有定义 若
上有定义 若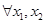
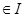 都有
都有 则称
则称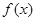 是区间
是区间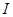 的向上凸函数;若
的向上凸函数;若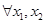
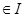 都有
都有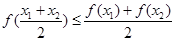 则称
则称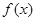 是区间
是区间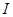 的向下凸函数. 有下列四个判断:
的向下凸函数. 有下列四个判断:
①若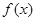 是区间
是区间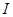 的向上凸函数,则
的向上凸函数,则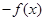 是区间
是区间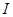 的向下凸函数;
的向下凸函数;
②若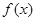 和
和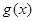 都是区间
都是区间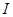 的向上凸函数 则
的向上凸函数 则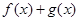 是区间
是区间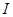 的向上凸函数;
的向上凸函数;
③若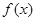 在区间
在区间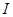 的向下凸函数且
的向下凸函数且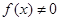 ,则
,则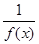 是区间
是区间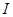 的向上凸函数;
的向上凸函数;
④若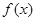 是区间
是区间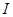 的向上凸函数,
的向上凸函数,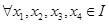 则有
则有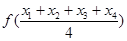
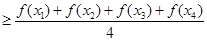
其中正确的结论个数是( )
| A.1 | B.2 | C.3 | D.4 |
①②
解析 试题分析:利用定义易知正确,③反例 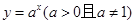
因为 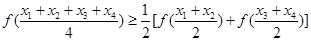
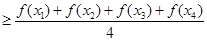 所以④正确.故填写①②。
所以④正确.故填写①②。
考点:函数的性质
点评:主要是对于新定义的理解和运用,属于中档题。
f=x+y+z是不是凸函数?就这种类似多个变量相加的多元函数是凸函数吗? 2020-05-13 …
已知凸函数的性质定理已知凸函数的性质定理:如果函数f(x)在区间D上是凸函数.已知凸函数的性质定理 2020-05-16 …
二阶导数与函数的凹凸性问题为什么二阶导数大于0,函数是凹函数.二阶导数小于0,函数是凸函数?能从本 2020-06-10 …
f(x1,x2)=(x1+x2)^2+e^(x1+x2)是不是凸函数怎样证明具体过程,要用凸集的方 2020-07-02 …
怎样判断一个函数是凸函数还是凹函数f(x)=LOGa(x)如果从图像上是判断不出是凸还是凹,那么有 2020-07-02 …
证明,若函数f(u)是单调增加的凸函数,函数u=V(x)是凸函数,则f[v(x)]也凸函数. 2020-07-14 …
1.两个凸函数的乘积是凸函数吗?如果是的话,证明这一点,如果不是,给一个反例2.证明,两个凸函数的 2020-07-29 …
高等数学题.请高人指点.利用f(x)=-lnx(x>0)是凸函数证明:当xi>0(i=1,2,.. 2020-07-29 …
凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对D内的任意x1,x2,…,xn都有f( 2020-08-02 …
凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意,,…,,有,已知函数 2020-08-02 …