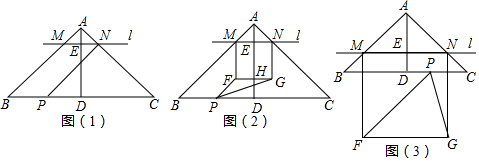
如图（1），在△ABC中，AB=AC，∠BAC=90°，AD⊥BC于点D，BC=20cm，AD=10cm．点P从点B出发，在线段BC上以每秒2cm的速度向点C匀速运动，与此同时，垂直于AD的直线l从点A沿AD出发，以每秒1cm的速度沿AD

Question

如图（1），在△ABC中，AB=AC，∠BAC=90°，AD⊥BC于点D，BC=20cm，AD=10cm．点P从点B出发，在线段BC上以每秒2cm的速度向点C匀速运动，与此同时，垂直于AD的直线l从点A沿AD出发，以每秒1cm的速度沿AD方向匀速平移，分别交AB、AC、AD于M、N、E．当点P到达点C时，点P与直线l同时停止运动，设运动时间为t秒（t>0）．
（1）在运动过程中（点P不与B、C重合），连接PN，求证：四边形MBPN为平行四边形；
（2）如图（2），以MN为边向下作正方形MFGN，FG交AD于点H，连结PF、PG，当0<t<(10)/(3)时，求△PFG的面积最大值；
（3）在整个运动过程中，观察图（2）、（3），是否存在某一时刻t，使△PFG为等腰三角形？若存在，直接写出t的值；若不存在，请说明理由．

Answer 1

（1）证明：∵l⊥AD，BC⊥AD，
∴l∥BC，
∴(AM)/(AB)=(AN)/(AC)，
∵AB=AC，
∴AM=AN，∵∠BAC=90°，
∴ME=NE，
∴MN=2AE=2t，
∵BP=2t，
∴MN=BP，
∴四边形MBPN为平行四边形；

（2） ∵四边形MFGN是正方形，
∴FG=MN=MF=2AE=2t，
∵EH=MF=2t，
∴DH=AD-AH=10-3t，
∴S_△PFG=(1)/(2)FG•DH=(1)/(2)×2t×（10-3t）=-3（t-(5)/(3)）²+(25)/(3)，
∵a=-3<0，0<t<(10)/(3)，
∴当t=(5)/(3)时，S_△PFG最大=(25)/(3)；

（3） 存在，当t=(30±10√(2))/(7)或t=5或t=10时，△PFG为等腰三角形；理由如下：
利用勾股定理得：PF²=2（10-3t）²，PG²=（10-3t）²+（10-t）²，又FG²=（2t）²，
当PF=FG时，则2（10-3t）²=（2t）²，
解得：t=(30±10√(2))/(7)，
当PF=PG时，2（10-3t）²=（10-3t）²+（10-t）²，
解得：t=5，或t=0（舍去）；
当FG=PG时，（2t）²=（10-3t）²+（10-t）²，
解得：t=10，或t=(10)/(3)（舍去）；
综上所述，t=(30±10√(2))/(7)或t=5或t=10时，△PFG为等腰三角形．