早教吧作业答案频道 -->数学-->
如图,已知抛物线y=-x2+bx+3与x轴相交于点A和点B(点A在点B的左侧),与y轴交于点C,且OB=OC,点D是抛物线的顶点,直线AC和BD交于点E.(1)求点D的坐标;(2)联结CD、BC,求∠DBC余切值;(3
题目详情
如图,已知抛物线y=-x2+bx+3与x轴相交于点A和点B(点A在点B的左侧),与y轴交于点C,且OB=OC,点D是抛物线的顶点,直线AC和BD交于点E.
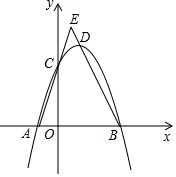
(1)求点D的坐标;
(2)联结CD、BC,求∠DBC余切值;
(3)设点M在线段CA延长线,如果△EBM和△ABC相似,求点M的坐标.

(1)求点D的坐标;
(2)联结CD、BC,求∠DBC余切值;
(3)设点M在线段CA延长线,如果△EBM和△ABC相似,求点M的坐标.
▼优质解答
答案和解析
(1)∵已知抛物线y=-x2+bx+3与y轴交于点C,
∴点C的坐标为:(0,3),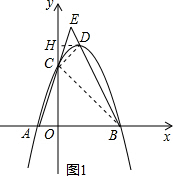
∵OB=OC,
∴点B的坐标为:(3,0),
∴-9+3b+3=0,
解得,b=2,
∴抛物线的解析式为:y=-x2+2x+3,
y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4);
(2)如图1,作DH⊥y轴于H,
则CH=DH=1,
∴∠HCD=∠HDC=45°,
∵OB=OC,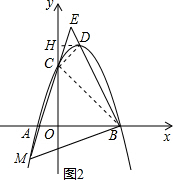
∴∠OCB=∠OBC=45°,
∴∠DCB=90°,
∴cot∠DBC=
=
=3;
(3)-x2+2x+3=0,
解得,x1=-1,x2=3,
∴点A的坐标为:(-1,0),
∴
=
,又
=
,
∴
=
,
∴Rt△AOC∽Rt△DCB,
∴∠ACO=∠DBC,
∵∠ACB=∠ACO+45°=∠DBC+∠E,
∴∠E=45°,
∵△EBM和△ABC相似,∠E=∠ABC=45°,
∴∠ACB=∠BME,
∴BM=BC,
设直线CA的解析式为:y=kx+b,
则
,
解得,
,
则直线CA的解析式为:y=3x+3,
设点M的坐标为(x,3x+3),
则(x-3)2+(3x+3)2=18,
解得,x1=0(舍去),x2=-
,
x2=-
时,y=-
,
∴点M的坐标为(-
,-
∴点C的坐标为:(0,3),

∵OB=OC,
∴点B的坐标为:(3,0),
∴-9+3b+3=0,
解得,b=2,
∴抛物线的解析式为:y=-x2+2x+3,
y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4);
(2)如图1,作DH⊥y轴于H,
则CH=DH=1,
∴∠HCD=∠HDC=45°,
∵OB=OC,

∴∠OCB=∠OBC=45°,
∴∠DCB=90°,
∴cot∠DBC=
| BC |
| DC |
3
| ||
|
(3)-x2+2x+3=0,
解得,x1=-1,x2=3,
∴点A的坐标为:(-1,0),
∴
| OA |
| OC |
| 1 |
| 3 |
| DC |
| BC |
| 1 |
| 3 |
∴
| OA |
| OC |
| DC |
| BC |
∴Rt△AOC∽Rt△DCB,
∴∠ACO=∠DBC,
∵∠ACB=∠ACO+45°=∠DBC+∠E,
∴∠E=45°,
∵△EBM和△ABC相似,∠E=∠ABC=45°,
∴∠ACB=∠BME,
∴BM=BC,
设直线CA的解析式为:y=kx+b,
则
|
解得,
|
则直线CA的解析式为:y=3x+3,
设点M的坐标为(x,3x+3),
则(x-3)2+(3x+3)2=18,
解得,x1=0(舍去),x2=-
| 6 |
| 5 |
x2=-
| 6 |
| 5 |
| 3 |
| 5 |
∴点M的坐标为(-
| 6 |
| 5 |
|
作业帮用户
2017-11-13

 |
看了 如图,已知抛物线y=-x2+...的网友还看了以下:
如图,△ABC中,AB=AC,AB的中垂线交BC于点E,D为垂足,如果角B=40°,求角BAE和角 2020-05-21 …
已知如图,在Rt△ABC中,角ACB=90度,AE平分角BAC交BC于点E,D为AC上的点,BE= 2020-06-03 …
e^x1-e^x2+1/ex^1-1/e^x2怎么等于(e^x2-e^x1)(1/e^x1e^2- 2020-06-12 …
如图,在△ABC中,AB=AC=5,BC=4,线段AB的垂直平分线分别交AB,AC于点E,D.求△ 2020-06-27 …
已知:如图,AB=AC,AB为圆O的直径,AC,BC分别交圆O于点E,D,连结ED,BE.求证DE 2020-07-21 …
设a>0,f(x)=e^x/a+a/e^x是R上的偶函数,证明:f(x)在(0,+无穷)上是增函数 2020-08-01 …
设随机向量(X1,X2,X3)间的相关系数分别为ρ12,ρ23,ρ31,且,E(X1)=E(X2) 2020-08-02 …
关于数理统计的问题,“总体”和“样本”为什么同分布?若X=X1+X2+...+Xn(X1..Xn独 2020-08-03 …
D为等边三角形ABC的AB边上的一点,作∠CDE=60°,DE交∠ABC的外角平分线于点E,D为等 2020-08-03 …
如图在三角形abc中ab的垂直平分线分别为交ab,bc于点e,d,ac的垂直平分线分别交ac,bc于 2020-11-21 …
 扫描下载二维码
扫描下载二维码