早教吧作业答案频道 -->数学-->
在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)(1)求证:∠BAD=∠EDC;(2)点E关于直线BC的对称点为M,连接DM,AM.①依题意将图2补全;②小姚通过观察,实验提出猜想:
题目详情
在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)
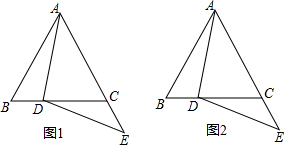
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②小姚通过观察,实验提出猜想:在点D运动的过程中,始终有DA=AM,小姚把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明DA=AM,只需证△ADM是等边三角形;
想法2:连接CM,只需证明△ABD≌△ACM即可.
请你参考上面的想法,帮助小姚证明DA=AM(一种方法即可)

(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②小姚通过观察,实验提出猜想:在点D运动的过程中,始终有DA=AM,小姚把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明DA=AM,只需证△ADM是等边三角形;
想法2:连接CM,只需证明△ABD≌△ACM即可.
请你参考上面的想法,帮助小姚证明DA=AM(一种方法即可)
▼优质解答
答案和解析
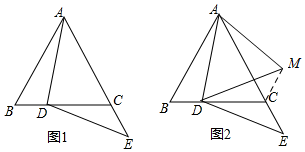 (1)如图1,∵DE=DA,
(1)如图1,∵DE=DA,
∴∠E=∠DAC,
∵△ABC是等边三角形,
∴∠BAC=∠ACD=60°,
即∠BAD+∠DAC=∠E+∠EDC=60°,
∴∠BAD=∠EDC;
(2)①补全图形如图2;
②证法1:由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°-∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°-120°=60°,
∴△ADN是等边三角形,
∴AD=AM;
证法2:连接CM,
由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°-∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°-120°=60°,
∴△ADM中,∠DAM=(180°-60°)÷2=60°,
又∵∠BAC=60°,
∴∠BAD=∠CAM,
由轴对称可得,∠DCE=∠DCM=120°,
又∵∠ACB=60°,
∴∠ACM=120°-60°=60°,
∴∠B=∠ACM,
在△ABD和△ACM中,
,
∴△ABD≌△ACM(ASA),
∴AD=AM.
 (1)如图1,∵DE=DA,
(1)如图1,∵DE=DA,∴∠E=∠DAC,
∵△ABC是等边三角形,
∴∠BAC=∠ACD=60°,
即∠BAD+∠DAC=∠E+∠EDC=60°,
∴∠BAD=∠EDC;
(2)①补全图形如图2;
②证法1:由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°-∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°-120°=60°,
∴△ADN是等边三角形,
∴AD=AM;
证法2:连接CM,
由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°-∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°-120°=60°,
∴△ADM中,∠DAM=(180°-60°)÷2=60°,
又∵∠BAC=60°,
∴∠BAD=∠CAM,
由轴对称可得,∠DCE=∠DCM=120°,
又∵∠ACB=60°,
∴∠ACM=120°-60°=60°,
∴∠B=∠ACM,
在△ABD和△ACM中,
|
∴△ABD≌△ACM(ASA),
∴AD=AM.
看了 在等边△ABC中,点D在BC...的网友还看了以下:
如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP沿CP翻折,点B的对应点B′恰好落在D 2020-05-13 …
在平行四边形ABCD中,AB=2BC,点E在DA的延长线上,AE=AD,点F在AD的延长线上,DF 2020-05-16 …
初二数学急急1.点p是平行四边形ABCD边AD的延长线上一点(如图),S△ABP、S△CDP、S△ 2020-05-24 …
如图①,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.(1)求∠DAE的度数;(2)如 2020-07-17 …
ABCD是圆的内接四边形,AC是圆的直径,BD垂直于AC,BD与AC的交点为E,F在DA的延长线上 2020-08-03 …
三角形ABC是圆O点的内接三角形,AC=BC,点D在弧AB上,点E在DA的延长线上,切CE=CD 2020-08-03 …
如图,等腰Rt△ABD中,AB=AD,点M为边AD上一动点,点E在DA的延长线上,且AM=AE,以B 2020-11-01 …
如图△ABC内接于圆O且AB=AC,点D在圆上AD⊥AB于点A,AD与BC交于点E,如图,△ABC内 2020-11-03 …
如图,△ABC内接于⊙O,且AB=AC,BD是⊙O的直径,AD与BC交于点E,F在DA的延长线上,且 2020-11-03 …
感知:如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°,求∠DAE度数 2020-11-27 …