早教吧作业答案频道 -->数学-->
F是双曲线x2a2-y2b2=1(a>0,b>0)的左焦点,过F作某一渐近线的垂线,分别与两条渐近线相交于A,B两点,若|AF||BF|=12
题目详情
F是双曲线
-
=1(a>0,b>0)的左焦点,过F作某一渐近线的垂线,分别与两条渐近线相交于A,B两点,若
=
,则双曲线的离心率为___.
| x2 |
| a2 |
| y2 |
| b2 |
| |AF| |
| |BF| |
| 1 |
| 2 |
▼优质解答
答案和解析
当b>a>0时,由
=
,可知A为BF的中点,由条件可得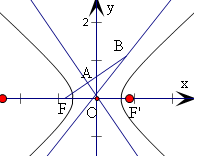
=
,
则Rt△OAB中,∠AOB=
,
渐近线OB的斜率k=
,
即离心率e=
=
=2.
同理当a>b>0时,可得e=
;
故答案为:
或2.
| |AF| |
| |BF| |
| 1 |
| 2 |

| |OA| |
| |OB| |
| 1 |
| 2 |
则Rt△OAB中,∠AOB=
| π |
| 3 |
渐近线OB的斜率k=
| 3 |
即离心率e=
| c |
| a |
| 1+3 |
同理当a>b>0时,可得e=
| 2 |
| 3 |
| 3 |
故答案为:
| 2 |
| 3 |
| 3 |
看了 F是双曲线x2a2-y2b2...的网友还看了以下:
已知双曲线x2a2−y2b2=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OA 2020-04-08 …
已知双曲线x2a2−y2b2=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OA 2020-05-13 …
已知双曲线x2a2−y2b2=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OA 2020-05-13 …
双曲线x²/a²-y²/b²=1的右准线与两条渐近线交与A、B两点(求详解TT)双曲线x²/a²- 2020-06-16 …
已知双曲线x2a2-y2b2=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OA 2020-06-16 …
著名诗人黄遵宪在《今别离》一诗中写到:“别肠转如轮,一刻既万周;眼见双轮驰,益增心中忧……送者未及 2020-06-18 …
已知双曲线x2a2-y2b2=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OA 2020-06-27 …
如图,已知椭圆,双曲线(a>0,b>0),若以C1的长轴为直径的圆与C2的一条渐近线交于A,B两点 2020-07-20 …
已知双曲线x2a2-y2b2=1(a>0,b>0),过其右焦点F且与渐近线y=-bax平行的直线分 2020-08-01 …
过双曲线X²/a²-Y²/b²=1(a>0,b>0)的右焦点F2作斜率为1的直线L,直线L与双曲线 2020-08-01 …