如图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80～90分数段的学员数为21人（Ⅰ）求该专业毕业总人数N和90～95分数段内的人数n；（Ⅱ）现欲将90～95分数段内

Question

如图为某校语言类专业N名毕业生的综合测评成绩（百分制）分布直方图，已知80～90分数段的学员数为21人

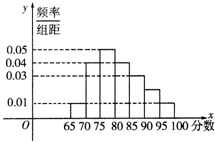
（Ⅰ）求该专业毕业总人数N和90～95分数段内的人数n；
（Ⅱ）现欲将90～95分数段内的n名毕业生分配往甲、乙、丙三所学校，若向学校甲分配两名毕业生，且其中至少有一名男生的概率为(3)/(5)，求n名毕业生中男女各几人（男女人数均至少两人）？
（Ⅲ）在（Ⅱ）的结论下，设随机变量ξ表示n名毕业生中分配往乙学校的三名学生中男生的人数，求ξ的分布列和数学期望．

Answer 1

（Ⅰ）80～90分数段的毕业生的频率为：
p₁=（0.04+0.03）×5=0.35，
此分数段的学员总数为21人，
∴毕业生的总人数N为N=(21)/(0.35)=60，
90～95分数段内的人数频率为：
p₂=1-（0.01+0.04+0.05+0.04+0.03+0.01）×5=0.1，
∴90～95分数段内的人数n=60×0.1=6．
（Ⅱ）90：95分数段内共6名毕业生，设其中男生z名，女生为6-x名
设分配往甲校的两名毕业生中至少有一名男毕业生为事件A，
则P（A）=1-(C26-x)/(C26)=(3)/(5)，
解得x=2或x=9（舍去），
即6名毕业生中有男生2人，女生4人．…（8分）
（Ⅲ）ξ表示n名毕业生中分配往甲学校的两名学生中男生的人数，
所以ξ的取值可以为0，1，2，
当ξ=0时，P（ξ=0）=(C34)/(C36)=(1)/(5)，
当ξ=1时，P（ξ=1）=(C12C24)/(C36)=(3)/(5)，
当ξ=2时，P（ξ=2）=(C22C14)/(C36)=(1)/(5)，
所以ξ的分布列为

ξ	0	1	2
P	(1)/(5)	(3)/(5)	(1)/(5)

所以随机变量ξ数学期望为Eξ=0×(1)/(5)+1×(3)/(5)+2×(1)/(5)=1．…（12分）