早教吧作业答案频道 -->数学-->
已知二次函数y=ax2+bx+c(a≠0)图象如图,有下列8个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数);⑥2a+b=0;⑦b2-4ac≤0;⑧(a+c)2>b2其中正确的结论
题目详情
已知二次函数y=ax2+bx+c(a≠0)图象如图,有下列8个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数);⑥2a+b=0;⑦b2-4ac≤0;⑧(a+c)2>b2
其中正确的结论有___.
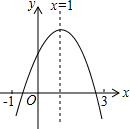
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数);⑥2a+b=0;⑦b2-4ac≤0;⑧(a+c)2>b2
其中正确的结论有___.
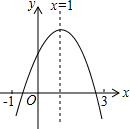
▼优质解答
答案和解析
①由抛物线的开口方向向下可推出a<0,
因为对称轴在y轴右侧,对称轴为x=-
>0,
而a<0,所以b>0,
由抛物线与y轴的交点在y轴的正半轴上,可知c>0,故abc<0,错误;
②当x=-1时,y<0,∴a-b+c<0,a+c<b,错误;
③当x=2时,y>0,∴4a+2b+c>0,正确;
④对称轴为x=-
=1,∴a=-
,∵a-b+c<0,∴-
-b+c<0,∴2c<3b,正确;
⑤∵当x=1时有最大值y=a+b+c,∴a+b+c>am2+bm+c,∴a+b>m(am+b)(m≠1的实数),正确;
⑥对称轴为x=-
=1,∴b=-2a,∴2a+b=0,正确;
⑦抛物线与x轴有两个交点,∴b2-4ac>0,错误;
⑧∵x=1时,y=a+b+c>0,x=-1时,y=a-b+c<0,
∴(a+b+c)(a-b+c)<0,
即[(a+c)+b][(a+c)-b]=(a+c)2-b2<0,
∴(a+c)2<b2,正确..
综上可得:③④⑤⑥⑧正确.
故答案为③④⑤⑥⑧.
因为对称轴在y轴右侧,对称轴为x=-
| b |
| 2a |
而a<0,所以b>0,
由抛物线与y轴的交点在y轴的正半轴上,可知c>0,故abc<0,错误;
②当x=-1时,y<0,∴a-b+c<0,a+c<b,错误;
③当x=2时,y>0,∴4a+2b+c>0,正确;
④对称轴为x=-
| b |
| 2a |
| b |
| 2 |
| b |
| 2 |
⑤∵当x=1时有最大值y=a+b+c,∴a+b+c>am2+bm+c,∴a+b>m(am+b)(m≠1的实数),正确;
⑥对称轴为x=-
| b |
| 2a |
⑦抛物线与x轴有两个交点,∴b2-4ac>0,错误;
⑧∵x=1时,y=a+b+c>0,x=-1时,y=a-b+c<0,
∴(a+b+c)(a-b+c)<0,
即[(a+c)+b][(a+c)-b]=(a+c)2-b2<0,
∴(a+c)2<b2,正确..
综上可得:③④⑤⑥⑧正确.
故答案为③④⑤⑥⑧.
看了 已知二次函数y=ax2+bx...的网友还看了以下:
已知关于X的一元二次方程x^2+2(k-1)x+k^2-1=0有两个不相等的实数根已知关于x的一元 2020-05-16 …
已知f(x)=3^(x-b)(2≤x≤4)的图像过点(2,1),则f(x)的值域为多少?f(2)= 2020-06-02 …
先阅读,设a、b是有理数,且满足a+√2▔·b=3-2√2▔,求b的a次方的值.由题意得(a-3) 2020-06-14 …
已知函数f(x)的定义域为[0,2],则函数g(x)=f(x+1/2)+f(x-1/2)的定义域为 2020-06-25 …
a和b都是向量,下列说法正确的是()?A、(a+b)(a-b)=▏a▕ˆ2-▏b▕ˆ2B、a•(a 2020-07-09 …
已知(a,b)=12,[a,b]=180:(1)a=60,b=36;(2)a=12,b=180正确 2020-07-16 …
一条数学题,求高手详解,谢谢!点A(3,0),B(1,-2)且lABl=4,求动点M到AB两点距离 2020-07-16 …
(x-2)^2=9(x+3)(步骤)用十字相乘法:x^2-5倍的根号2*x+83x^2-2x-1= 2020-08-03 …
△ABC中,角A,B,C的对边分别为a,b,c,且a^2-(b-c)^2=(2-√3)bc,和sin 2020-10-30 …
已知△ABC的三个顶点分别为A(1,0),B(2,2),C(0,4),求cosA与cosB的绝对值. 2020-12-31 …