如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF，则下列结论：①△EBF≌△DFC；②四边形AEFD为平行四边形；③当AB=AC，∠BAC=120°时，四边形AEFD是正方形．其中正确的结论是．（请

Question

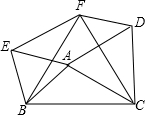
如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF，则下列结论：①△EBF≌△DFC；②四边形AEFD为平行四边形；③当AB=AC，∠BAC=120°时，四边形AEFD是正方形．其中正确的结论是___．（请写出正确结论的序号）．

Answer 1

∵△ABE、△BCF为等边三角形，
∴AB=BE=AE，BC=CF=FB，∠ABE=∠CBF=60°，
∴∠ABE-∠ABF=∠FBC-∠ABF，即∠CBA=∠FBE，
在△ABC和△EBF中，

AB=EB

∠CBA=∠FBE

BC=BF

，
∴△ABC≌△EBF（SAS），
∴EF=AC，
又∵△ADC为等边三角形，
∴CD=AD=AC，
∴EF=AD=DC，
同理可得△ABC≌△DFC，
∴DF=AB=AE=DF，
∴四边形AEFD是平行四边形，选项②正确；
∴∠FEA=∠ADF，
∴∠FEA+∠AEB=∠ADF+∠ADC，即∠FEB=∠CDF，
在△FEB和△CDF中，

EF=DC

∠FEB=∠CDF

EB=FD

．
∴△FEB≌△CDF（SAS），选项①正确；
若AB=AC，∠BAC=120°，则有AE=AD，∠EAD=120°，此时AEFD为菱形，选项③错误，
故答案为：①②．