早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=12x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).(1)求抛物线的解析式;(2)若P是直线AB上方该抛物线上的一个动
题目详情
如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
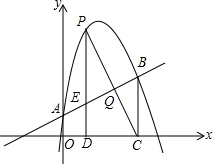
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
| 1 |
| 2 |

(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
▼优质解答
答案和解析
(1)∵BC⊥x轴,垂足为点C(4,0),且点B在直线y=
x+1上,
∴点B的坐标为:(4,3),
∵抛物线y=ax2+bx+1经过点(2,6)和点B(4,3),
∴
,
解得:
,
故抛物线的解析式为:y=-x2+
x+1;
(2)如图所示:设动点P的坐标为;(x,-x2+
x+1),
则点E的坐标为:(x,
x+1),
∵PD⊥x轴于点D,且点P在x轴上,
∴PE=PD-ED=(-x2+
x+1)-(
x+1)
=-x2+4x
=-(x-2)2+4,
则当x=2时,PE的最大值为:4;
(3)∵PC与BE互相平分,
∴PE=BC,
∴-x2+4x=3,即x2-4x+3=0,
解得:x1=1,x2=3,
∵点Q分别时PC,BE的中点,且点Q在直线y=
x+1,
∴①当x=1时,点Q的横坐标为:
,∴点Q的坐标为:(
,
),
②当x=3时,点Q的横坐标为:
,∴点Q的坐标为:(
,
),
综上所述,点Q的坐标为:(
,
),(
,
).
| 1 |
| 2 |
∴点B的坐标为:(4,3),
∵抛物线y=ax2+bx+1经过点(2,6)和点B(4,3),
∴
|
解得:
|
故抛物线的解析式为:y=-x2+
| 9 |
| 2 |
(2)如图所示:设动点P的坐标为;(x,-x2+
| 9 |
| 2 |
则点E的坐标为:(x,
| 1 |
| 2 |

∵PD⊥x轴于点D,且点P在x轴上,
∴PE=PD-ED=(-x2+
| 9 |
| 2 |
| 1 |
| 2 |
=-x2+4x
=-(x-2)2+4,
则当x=2时,PE的最大值为:4;
(3)∵PC与BE互相平分,
∴PE=BC,
∴-x2+4x=3,即x2-4x+3=0,
解得:x1=1,x2=3,
∵点Q分别时PC,BE的中点,且点Q在直线y=
| 1 |
| 2 |
∴①当x=1时,点Q的横坐标为:
| 5 |
| 2 |
| 5 |
| 2 |
| 9 |
| 4 |
②当x=3时,点Q的横坐标为:
| 7 |
| 2 |
| 7 |
| 2 |
| 11 |
| 4 |
综上所述,点Q的坐标为:(
| 5 |
| 2 |
| 9 |
| 4 |
| 7 |
| 2 |
| 11 |
| 4 |
看了 如图,抛物线y=ax2+bx...的网友还看了以下:
1.一个有理数在数轴上对应的点为A,将A点向左移动3个单位长度,再向左移动2个单位长度,得到点B, 2020-04-08 …
已知点P是一次函数Y=3X-6的图像上的一点,并且点P到X轴,Y轴的距离相等,求点P的坐标 2020-05-16 …
坐标系中,已知点A(-2,0),B(0,4),C(0,3),过点C交x轴于点D,使得以D,O,C为 2020-06-03 …
已知正比例函数y1=k1x和反比例函数y2=k1/x(k1k2≠0),都过A(1,根号3),求y1 2020-06-14 …
已知抛物线y=ax2-x+c过点A(-6,0),与Y轴交与点B,顶点为D,对称轴是直线x=-2(1 2020-06-14 …
已知一次函数y=3x+3的图像与x轴交于点A与y轴交于点B又二次函数y=-x^2+bx+c的图像经 2020-06-14 …
1.一个有理数在数轴上的对应点为A,将A点先向右移动5个单位长度,再向左移动4个单位长度得到点B, 2020-06-27 …
快开学了,1)将平行四边形ABCD的对角线交点与直角坐标系的原点重合,且点A,B的坐标分别为(-2 2020-07-04 …
数轴上两点A,B对应的数分别为-1,4,点P为数轴上一动点,其对应的数为x(1)若点P到点A,点B 2020-07-16 …
已知直线y=-x+3交x轴于点B,抛物线y=ax^2+bx+c经过A,B,C(1,0)三点1.点D的 2020-11-01 …