早教吧作业答案频道 -->数学-->
阅读下列材料:利用完全平方公式,可以将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.运用多项式的配方法及平方差公式能对一些多项
题目详情
阅读下列材料:
利用完全平方公式,可以将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+11x+24=x2+11x+(
)2-(
)2+24
=(x+
)2-
=(x+
+
)(x+
-
)
=(x+8)(x+3)
根据以上材料,解答下列问题:
(1)用多项式的配方法将x2+8x-1化成(x+m)2+n的形式;
(2)下面是某位同学用配方法及平方差公式把多项式x2-3x-40进行分解因式的解答过程:
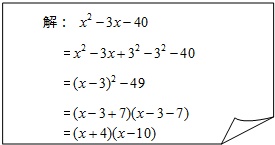
老师说,这位同学的解答过程中有错误,请你找出该同学解答中开始出现错误的地方,并用“”标画出来,然后写出完整的、正确的解答过程:
(3)求证:x,y取任何实数时,多项式x2+y2-2x-4y+16的值总为正数.
利用完全平方公式,可以将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+11x+24=x2+11x+(
| 11 |
| 2 |
| 11 |
| 2 |
=(x+
| 11 |
| 2 |
| 25 |
| 4 |
=(x+
| 11 |
| 2 |
| 5 |
| 2 |
| 11 |
| 2 |
| 5 |
| 2 |
=(x+8)(x+3)
根据以上材料,解答下列问题:
(1)用多项式的配方法将x2+8x-1化成(x+m)2+n的形式;
(2)下面是某位同学用配方法及平方差公式把多项式x2-3x-40进行分解因式的解答过程:
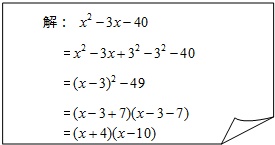
老师说,这位同学的解答过程中有错误,请你找出该同学解答中开始出现错误的地方,并用“”标画出来,然后写出完整的、正确的解答过程:
(3)求证:x,y取任何实数时,多项式x2+y2-2x-4y+16的值总为正数.
▼优质解答
答案和解析
(1)x2+8x-1
=x2+8x+42-42-1
=(x+4)2-17;
(2)如图所示:
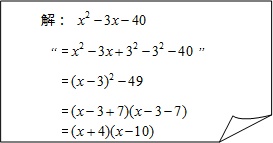
正确的解答过程:
x2-3x-40=x2-3x+(
)2-(
)2-40
=(x-
)2-
=(x-
+
)(x-
-
)
=(x+5)(x-8);
(3)证明:x2+y2-2x-4y+16=(x2-2x+1)+(y2-4y+4)+11=(x-1)2+(y-2)2+11≥11,
故x,y取任何实数时,多项式x2+y2-2x-4y+16的值总为正数.
=x2+8x+42-42-1
=(x+4)2-17;
(2)如图所示:
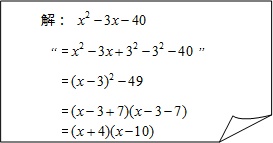
正确的解答过程:
x2-3x-40=x2-3x+(
| 3 |
| 2 |
| 3 |
| 2 |
=(x-
| 3 |
| 2 |
| 169 |
| 4 |
=(x-
| 3 |
| 2 |
| 13 |
| 2 |
| 3 |
| 2 |
| 13 |
| 2 |
=(x+5)(x-8);
(3)证明:x2+y2-2x-4y+16=(x2-2x+1)+(y2-4y+4)+11=(x-1)2+(y-2)2+11≥11,
故x,y取任何实数时,多项式x2+y2-2x-4y+16的值总为正数.
看了 阅读下列材料:利用完全平方公...的网友还看了以下:
已知a,b,c均为整数,且a-b的绝对值的三次方+c-a的绝对值的平方=1,求a-c的绝对值+c- 2020-04-05 …
如果A=2x的5次方-3x的平方乘y的3次方+2y的5次方,B=2x的平方+xy-3y的平方,C= 2020-05-14 …
■在线等!高一数学,数列证明■已知a,b,c,d成等比数列(公比为q),求怔:(1)如果q≠-1, 2020-05-14 …
在有理数范围内,下列多项式能用公式法进行因式分解的是A.a的平方-6a B.a的平方-ab+b的平 2020-05-16 …
人民解放军进行军事演习时在海拔高度为600M的某海岛顶端A处设立了一个观察点上午九时观察员发现“红 2020-05-16 …
以知一元二次方程ax2+bx+c=0的一个根为1,以知一元二次方程ax²+bx+c=0的一个根为1 2020-05-16 …
整式的乘法的比赛题.第一题:已知,2的a次方=5,2的b次方=6,求2的3a+2b次方?第二题:已 2020-05-19 …
已知a,b,c均为整数,且a-b的绝对值的三次方+c-a的绝对值的平方=1,求a-c的绝对值+c- 2020-06-24 …
A.屋舍俨然B.满目萧然C.百事也尽然D.望之蔚然而深秀者,琅玡也各位大哥,你们好!这四句中的“然 2020-06-29 …
1.若a、b、c均为整数,且|a-b|的立方+|c-a|的平方=1,求|a-c|+|c-b|+|b 2020-07-09 …