早教吧作业答案频道 -->数学-->
如图,在△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=90°,将△DCE绕点C旋转(0°<∠ACD<180°),连结BD和AE:(1)求证:△BCD≌△ACE;(2)试确定线段BD和AE的数量关系和位置关系;(3)连接A
题目详情
如图,在△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=90°,将△DCE绕点C旋转(0°<∠ACD<180°),连结BD和AE:
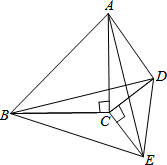
(1)求证:△BCD≌△ACE;
(2)试确定线段BD和AE的数量关系和位置关系;
(3)连接AD和BE,在旋转过程中,△ACD的面积记为S1,△BCE的面积记为S2,试判断S1和S2的大小,并给予证明.

(1)求证:△BCD≌△ACE;
(2)试确定线段BD和AE的数量关系和位置关系;
(3)连接AD和BE,在旋转过程中,△ACD的面积记为S1,△BCE的面积记为S2,试判断S1和S2的大小,并给予证明.
▼优质解答
答案和解析
 (1)证明:∵∠ABC=∠DCE=90°,
(1)证明:∵∠ABC=∠DCE=90°,
∴∠ABC+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△BCD与△ACE中
∴△BCD≌△ACE(SAS);
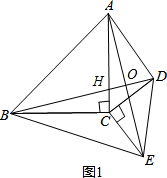
(2) 如图1,∵△BCD≌△ACE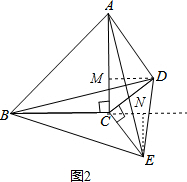
∴BD=AE,∠DBC=∠EAC
∵∠AHO=∠BHC
∴∠AHO+∠EAC=∠BHC+∠DBC=90°
∴∠AOH=90°
∴BD⊥AE
(3) 如图2,作DM⊥AC于M,EN⊥BC于N,
∵∠MCD+∠DCN=90°,∠ECN+∠DCN=90°,
∴∠MCD=∠NCE,
在△DCM和△ECN中
∴△DCM≌△ECN(AAS),
∴DM=EN,
∵S1=
AC•DM,S2=
BC•EN,
∵AC=BC,
∴S1=S2.
 (1)证明:∵∠ABC=∠DCE=90°,
(1)证明:∵∠ABC=∠DCE=90°,∴∠ABC+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE,
在△BCD与△ACE中
|
∴△BCD≌△ACE(SAS);
(2) 如图1,∵△BCD≌△ACE

∴BD=AE,∠DBC=∠EAC
∵∠AHO=∠BHC
∴∠AHO+∠EAC=∠BHC+∠DBC=90°
∴∠AOH=90°
∴BD⊥AE
(3) 如图2,作DM⊥AC于M,EN⊥BC于N,
∵∠MCD+∠DCN=90°,∠ECN+∠DCN=90°,
∴∠MCD=∠NCE,
在△DCM和△ECN中
|
∴△DCM≌△ECN(AAS),
∴DM=EN,
∵S1=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC=BC,
∴S1=S2.
看了 如图,在△ABC和△DCE中...的网友还看了以下:
如图中,按照生物体的结构层次排序,正确的图形排列是()A.a→b→c→d→eB.c→e→a→d→b 2020-05-02 …
( )3.设一个栈的输入序列为A,B,C,D,则借助一个栈所得到的输出序列不可能是_______. 2020-05-17 …
一个栈的入栈序列是a b c d e,则栈不可能的输出序列是( )。A.e d c b a B.d 2020-05-23 …
(a+b+c+d)(a+b-c-d)(a+c-b-d)(c+b-a-d)+16abcd因式分解 2020-06-27 …
下列卤化物在浓的KOH醇溶液中脱卤化氢的反应速度最快的是?选项为:a)1-溴戊烷b)2-溴戊烷c) 2020-06-28 …
已知A2-、B-、C+、D2+、E3+五种简单离子的核外电子数相等,则它们对应的核电荷数由大到小的 2020-07-09 …
如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村 2020-11-05 …
如图,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送 2020-11-05 …
读“丹霞地貌形成示意图”,回答下列各题:1.丹霞地貌的形成过程正确的是()A.c→b→d→a→f→e 2020-11-21 …
某公路的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→ 2020-11-22 …