早教吧作业答案频道 -->数学-->
探究如图①,分别以△ABC的两边AB和AC为边向△ABC外作正三角形ABD和正三角形ACE,连结DC、BE,求证:DC=BE.拓展如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD,若∠DAC=90°
题目详情
【探究】如图①,分别以△ABC的两边AB和AC为边向△ABC外作正三角形ABD和正三角形ACE,连结DC、BE,求证:DC=BE.
【拓展】如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD,若∠DAC=90°,AC=AD,则BD的长为___.
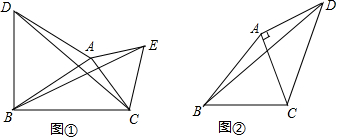
【拓展】如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD,若∠DAC=90°,AC=AD,则BD的长为___.

▼优质解答
答案和解析
【探究】∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴CD=BE;
【拓展】如图②,以AB为边向外作等腰直角三角形AB,AE=AB,∠BAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ACE≌△ABD,
∴CE=BD,
∵BE=
AB=5
,
∵∠ABC=45°,
∴∠EBC=90°,
∴CE=
=5
,
∴BD=5
,
故答案为:5
.
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
|

∴△DAC≌△BAE(SAS),
∴CD=BE;
【拓展】如图②,以AB为边向外作等腰直角三角形AB,AE=AB,∠BAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ACE≌△ABD,
∴CE=BD,
∵BE=
| 2 |
| 2 |
∵∠ABC=45°,
∴∠EBC=90°,
∴CE=
| BE2+BC2 |
| 3 |
∴BD=5
| 3 |
故答案为:5
| 3 |
看了 探究如图①,分别以△ABC的...的网友还看了以下:
现有5个边长为1的小正方形如图④所示,请在图④中画出合适的分割线,使分割后的部分能拼成一个新正方形 2020-05-17 …
右图由正五边形构成,在图1中有5个点,图2中有12个右图由正五边形构成,在图1中有5个点,图2中有 2020-06-16 …
如图5-5-4所示,一个物体以速度v0冲向竖直墙壁,墙壁和物体间的弹簧被物体压缩,在此过程中以下说 2020-06-23 …
如右图,大正方形是由七巧板拼成的,每个图形的面积各占大正方形面积的几分之几?图形5和图形6共占大正 2020-06-27 …
图1是对酶的某种特性的解释模型,图2、3、4、5、6、7是在不同条件下某种酶促反应的变化情况,据图 2020-07-11 …
如图,正方形OABC和正方形ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y=1 2020-07-30 …
如图:正方形的边长是1个单位长度,四个顶点分别标有数字0,1,2,3按下列方法将数轴的正半轴绕在正 2020-08-02 …
如图:正方形的边长是1个单位长度,四个顶点分别标有数字0,1,2,3按下列方法将数轴的正半轴绕在正 2020-08-02 …
图5为某时期某地正午日影长短变化及朝向示意图。读图5,回答9、10题。图5 2020-12-01 …
如图,是由5×5个边长相同的小正方形组成的方格图,每个小正方形中都填了一个正整数.(1)观察方格图中 2021-02-05 …