早教吧作业答案频道 -->数学-->
如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.(1)求证:△ACE≌△BCD;(2)求证:BF⊥AE;(3)请判断∠CFE与∠CAB的大小关系并说明理由.
题目详情
如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
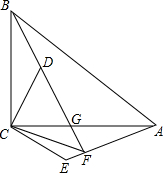
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.

(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
▼优质解答
答案和解析
证明:(1)∵BC⊥CA,DC⊥CE,
∴∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△BCD≌△ACE;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGE,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB,
过C作CH⊥AE于H,CI⊥BF于I,
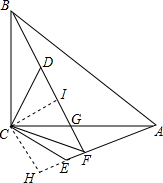 ∵△BCD≌△ACE,
∵△BCD≌△ACE,
∴AE=BD,S△ACE=S△BCD,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
∴∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
|
∴△BCD≌△ACE;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGE,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB,
过C作CH⊥AE于H,CI⊥BF于I,
 ∵△BCD≌△ACE,
∵△BCD≌△ACE,∴AE=BD,S△ACE=S△BCD,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
看了 如图,BC⊥CA,BC=CA...的网友还看了以下:
● 在 SET 认证机构体系中, (40) 是离线并被严格保护的。 (40)A.商户 CA B.支付 2020-05-26 …
a-b+c=a+c-ba+(b-c)=a+b-ca-(b+c)=a-b-ca-(b-c)=a-b+ 2020-06-10 …
若a、b、c、d都是正数,则在以下命题中,错误的是()A.若a2+b2+c2=ab+bc+ca,则 2020-07-09 …
A、B、C、D能组成多少种不一样的?就是类似于A.C.B.DA.D.B.CA.D.C.B或者B开头 2020-07-25 …
根据a×b=c×d(a、b、c、d都不等于0),写成比例式是()A.ab=cdB.ac=bdC.b 2020-07-26 …
在△ABC和△A'B'C'中,已知∠C=∠C'=90°,点D,D'分别在边AB,A'B'上,且CD 2020-07-30 …
若a、b、c、d都是正数,则在以下命题中,错误的是()A.若a2+b2+c2=ab+bc+ca,则a 2020-10-31 …
高等代数的矩阵D证明题第一行ab00~00,第二行cab0~00,第三行0cab~00,最后一行00 2020-11-06 …
a和a′是一对同源染色体,由此类推,下列来自同一个精原细胞的精子是()A.ab′ca′bc′ab′c 2020-12-18 …
a和a′是一对同源染色体,由此类推,下列来自同一个精原细胞的精子是()A.ab′ca′bc′ab′c 2020-12-18 …