早教吧作业答案频道 -->数学-->
已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是:.(2)如图2,
题目详情
已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.
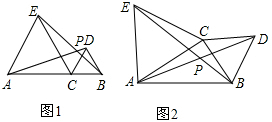
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是:___.
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE大小是否随着∠ACB的大小发生变化而发生变化,若变化写出变化规律,若不变,请求出∠APE的度数.

(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是:___.
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE大小是否随着∠ACB的大小发生变化而发生变化,若变化写出变化规律,若不变,请求出∠APE的度数.
▼优质解答
答案和解析
(1)∵△ACE和△BCD都是等边三角形,
∴∠ACE=∠DCB=60°,CA=CE,CD=CB,
∴∠ACE+∠DCE=∠DCB+∠DCE,即∠ACD=∠ECB,
在△ECB和△ACD中,
,
∴△ECB≌△ACD,
∴AD=BE,
故答案为:AD=BE;
(2)AD=BE成立.
证明:∵△ACE和△BCD是等边三角形,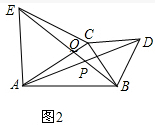
∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD,
在△ECB和△ACD中,
,
∴△ECB≌△ACD(SAS),
∴BE=AD;
(3)∠APE不随着∠ACB的大小发生变化,始终是60°,
如图2,设BE与AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC,
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°,
∴∠APQ=∠ECQ=60°,即∠APE=60°.
∴∠ACE=∠DCB=60°,CA=CE,CD=CB,
∴∠ACE+∠DCE=∠DCB+∠DCE,即∠ACD=∠ECB,
在△ECB和△ACD中,
|
∴△ECB≌△ACD,
∴AD=BE,
故答案为:AD=BE;
(2)AD=BE成立.
证明:∵△ACE和△BCD是等边三角形,

∴EC=AC,BC=DC,
∠ACE=∠BCD=60°,
∴∠ACE+∠ACB=∠BCD+∠ACB,即∠ECB=∠ACD,
在△ECB和△ACD中,
|
∴△ECB≌△ACD(SAS),
∴BE=AD;
(3)∠APE不随着∠ACB的大小发生变化,始终是60°,
如图2,设BE与AC交于Q,
由(2)可知△ECB≌△ACD,
∴∠BEC=∠DAC,
又∵∠AQP=∠EQC,∠AQP+∠QAP+∠APQ=∠EQC+∠CEQ+∠ECQ=180°,
∴∠APQ=∠ECQ=60°,即∠APE=60°.
看了 已知:C是线段AB所在平面内...的网友还看了以下:
如图所示,将△ABC沿x轴向左平移,AC边与y轴交于一点P(P不同于A,C两点),过P点作一直线与 2020-05-13 …
求曲面x^2+y^2=1/2 *z^2与平面x+y+z=2的交线在点(1,-1,2)处的切线与法平 2020-05-16 …
在平面直角坐标系中,已知抛物线y=-x²+bx+c与x轴交于点A,B(点A在点B的左侧),与y轴的 2020-05-16 …
平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于点A,B点A在点B的左侧,与y轴的正半轴 2020-05-16 …
微积分的几何应用求球面x²+y²+z²=6与抛物面z=x²+y²的交线在点(1,1,2)处的切线在 2020-06-10 …
平面x-y+z=2和曲面z=x2+y2的交线在点(1,1,2)处的切线方程是x−1−1=y−13= 2020-06-12 …
已知抛物线y=x2-4x+3与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M 2020-06-15 …
如图,正方形ABCD的边长为2a,H是以BC为直径的半圆上一点,过点H与半圆相切的直线交AB于点E 2020-07-31 …
如图,己知抛物线y=38x2-34x-3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C 2020-08-02 …
三角形ABC为等边三角形D为AC上一点BD的垂直平分线交AB于点E交BC于点F1.当D在AC上移动 2020-08-03 …