早教吧作业答案频道 -->数学-->
如图,己知抛物线y=38x2-34x-3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)求出点A,B,D的坐标;(2)如图,若线段OB在x轴上移动,且点O,B移动后的对应点为O′
题目详情
如图,己知抛物线y=
x2-
x-3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
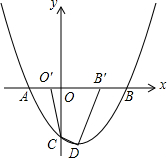
(1)求出点A,B,D的坐标;
(2)如图,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′,首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
| 3 |
| 8 |
| 3 |
| 4 |

(1)求出点A,B,D的坐标;
(2)如图,若线段OB在x轴上移动,且点O,B移动后的对应点为O′,B′,首尾顺次连接点O′、B′、D、C构成四边形O′B′DC,请求出四边形O′B′DC的周长最小值.
▼优质解答
答案和解析
(1)令y=0,则
x2-
x-3=0,解得x=-2或4,
∴点A坐标(-2,0),点B坐标(4,0).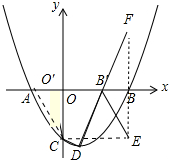
∵y=
x2-
x-3=
(x-1)2-
,
∴顶点D(1,-
).
(2)如图点C向右平移4个单位得到点E,点E关于x轴的对称点F坐标(4,3),连接DF与x轴交于点B′,此时四边形CDB′O′周长最小,
此时四边形CDB′O′周长=CD+CB′+B′O′+CO′=CD+O′B′+DB′+B′F=CD+O′B′+DF
=
+4+
=
+4+
.
| 3 |
| 8 |
| 3 |
| 4 |
∴点A坐标(-2,0),点B坐标(4,0).

∵y=
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 27 |
| 8 |
∴顶点D(1,-
| 27 |
| 8 |
(2)如图点C向右平移4个单位得到点E,点E关于x轴的对称点F坐标(4,3),连接DF与x轴交于点B′,此时四边形CDB′O′周长最小,
此时四边形CDB′O′周长=CD+CB′+B′O′+CO′=CD+O′B′+DB′+B′F=CD+O′B′+DF
=
12+(-
|
32+(-
|
| ||
| 8 |
3
| ||
| 8 |
看了 如图,己知抛物线y=38x2...的网友还看了以下:
C语言的一份习题3使用语句scanf(“x=%d,y=%d”,&x,&y);要使x,y的值均为3, 2020-05-13 …
如图,在直角坐标系中,抛物线y=ax^2+bx+c(a不等于0)与x轴交于点A(-1,0),B(3 2020-05-16 …
1.求当m为何值时,抛物线y=x^2-(m+3)x+4的定点在坐标轴上?2.已知抛物线y=x^2+ 2020-05-17 …
1.试写出一组实数X,Y,使log(3)X-log(3)Y=log(X-Y)成立,则X=,Y=.( 2020-05-23 …
抛物线y=ax-3ax+b经过A(-1,0),C(3,-2)两点,与y轴交于点D,与x轴交于另一点 2020-06-03 …
[高数的啊}忘了这几个题目怎么做了,求大师给个提示,提示就好验证下列各题中的函数是否为所给微分方程 2020-06-30 …
求解几道A国高中函数题,1)化简5丨3-i丨-丨4+2i√6丨答案=3根号10,2)x=(2y+3 2020-07-05 …
在三角形ABC中,abc分别是角ABC的对边,且8sin^2(B+C)/2-2cos2A=7,求角 2020-07-30 …
直线y=-3/4x+3与x轴y轴分别交于A,B两点,点C(X,Y)是y=-3/4x+3的动点过点C的 2021-01-10 …
求下列函数的值域(1)y=3x+1,x{1,2,3,4,5}(观察法)(2)y=x^2-x+6,x 2021-01-31 …