早教吧作业答案频道 -->数学-->
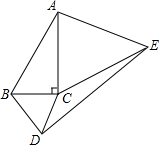
如图,分别以Rt△ABC的两条直角边为边向△ABC外作等边△BCD和等边△ACE,∠ACB=90°,∠BAC=30°,BC=1,求DE的长.
题目详情
如图,分别以Rt△ABC的两条直角边为边向△ABC外作等边△BCD和等边△ACE,∠ACB=90°,∠BAC=30°,BC=1,求DE的长.

▼优质解答
答案和解析
连接BE,如图所示: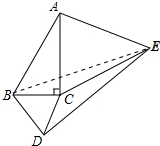
∵在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=1,
∴AB=2BC=2,AC=
=
=
,
∵△ACE为等边三角形,
∴∠CAE=∠ACE=60°,AC=AE=
,
∴∠BAE=∠BAC+∠CAE=30°+60°=90°,∠BCE=90°+60°=150°,
∴BE=
=
=
,
∵△BCD是等边三角形,
∴BC=CD,∠BCD=60°,
∴∠DCE=360°-150°-60°=150°=∠BCE,
在△BCE和△DCE中,
,
∴△BCE≌△DCE(SAS),
∴DE=BE=

∵在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=1,
∴AB=2BC=2,AC=
| AB2-BC2 |
| 22-12 |
| 3 |
∵△ACE为等边三角形,
∴∠CAE=∠ACE=60°,AC=AE=
| 3 |
∴∠BAE=∠BAC+∠CAE=30°+60°=90°,∠BCE=90°+60°=150°,
∴BE=
| AB2+AE2 |
22+(
|
| 7 |
∵△BCD是等边三角形,
∴BC=CD,∠BCD=60°,
∴∠DCE=360°-150°-60°=150°=∠BCE,
在△BCE和△DCE中,
|
∴△BCE≌△DCE(SAS),
∴DE=BE=
作业帮用户
2017-05-11

 |
看了 如图,分别以Rt△ABC的两...的网友还看了以下:
如图,在平面直角坐标系中,直线AB.CD分别与x轴、y轴交与A.B.C.D,点A(-2,0),B( 2020-05-15 …
已知平面a,b,r满足a垂直r,b垂直r,a交b=r,求证:l垂直r急 2020-06-15 …
如图,在磁感应强度为B的匀强磁场中,一直角边长度为a,电阻为R的等腰直角三角形导线框以速度v垂直于 2020-07-23 …
若直角三角形的两条直角边长度分别为a,b,则此三角形的外接圆半径r=a2+b22,运用类比方法,若 2020-07-31 …
如图所示,虚线区域内有一垂直纸面向里的匀强磁场,磁场宽度为L,磁感应强度大小为B.总电阻为R的直角 2020-07-31 …
已知点P是△ABC所在平面内的一点,边AB的中点为D,若2PD=(1-λ)PA+CB,其中λ∈R, 2020-07-31 …
勾股定理的证明这样可以不我们同学像这样证明做一直角三角形直角边为a,b,斜边为c,在做其内切圆,做 2020-08-02 …
如图所示,ABCD区域中存在一个垂直纸面向里的有界匀强磁场,磁感应强度为B,BC边距地面高度L2,正 2020-11-01 …
设直角边为xy则x+y+15=36x^2+y^2=15^2解得x=9设直角边为xy则x+y+15=3 2020-11-01 …
Rt△内切圆半径与边的关系的证明,直角三角形两直角边长分别为a,b.斜边为c,内切圆半径为r,求证r 2021-01-22 …
 扫描下载二维码
扫描下载二维码