早教吧作业答案频道 -->数学-->
己知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.①求证:
题目详情
己知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,FA,FD之间的数量关系,并证明你的结论:
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的同侧时,利用图2画出图形探究线段FE,FA,FD之间的数量关系,并直接写出你的结论.
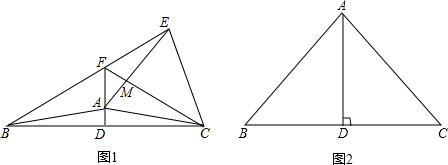
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,FA,FD之间的数量关系,并证明你的结论:
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的同侧时,利用图2画出图形探究线段FE,FA,FD之间的数量关系,并直接写出你的结论.

▼优质解答
答案和解析
(1)①∵AD⊥BC,AB=AC,
∴BD=DC,
∴FB=FC,
∴∠FBC=∠FCB,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠FBA=∠FCA,
∵以AC为边作等边三角形ACE,
∴AE=AC=AB,
∴∠ABF=∠AEF,
∴∠ACF=∠AEF,
即:∠FEA=∠FCA;
②结论:EF=2FD-AF,
∵以AC为边作等边三角形ACE,
∴∠EAC=60°,
由①有,∠ACF=∠AEF,
∴∠EFC=∠EAC=60°,
由①得,BF=CF,FD⊥BC,
∴∠BFD=∠CFD,
∵∠BFD+∠CFD+∠EFC=180°,
∴∠BFD=∠CFD=
=60°,
∴∠FCD=90°-∠CFD=30°,
∴∠ACD+∠ACF=30°,
∴∠ECF=∠ECA-∠ACF=60°-∠ACF=60°-(30°-∠ACD)=30°+∠ACD,
如图1,
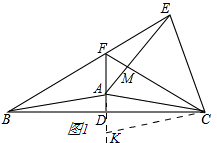
延长AD,在AD上截取AD=DK,连接CK,
∵AD⊥BC,
∴∠ACD=∠KCD,CA=CK
∴∠FCK=∠FCD+∠KCD=∠ACF+∠ACD+∠KCD=30°+∠KCD=30°+∠ACD,
∴∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
,
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FD-AF;
(2)②结论:EF=2FA-FD,
如图2,
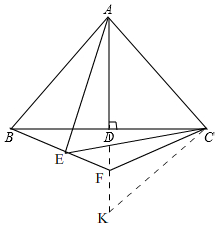
同(1)的方法得出∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
,
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FA-FD;
∴BD=DC,
∴FB=FC,
∴∠FBC=∠FCB,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠FBA=∠FCA,
∵以AC为边作等边三角形ACE,
∴AE=AC=AB,
∴∠ABF=∠AEF,
∴∠ACF=∠AEF,
即:∠FEA=∠FCA;
②结论:EF=2FD-AF,
∵以AC为边作等边三角形ACE,
∴∠EAC=60°,
由①有,∠ACF=∠AEF,
∴∠EFC=∠EAC=60°,
由①得,BF=CF,FD⊥BC,
∴∠BFD=∠CFD,
∵∠BFD+∠CFD+∠EFC=180°,
∴∠BFD=∠CFD=
| 180°-∠EFC |
| 2 |
∴∠FCD=90°-∠CFD=30°,
∴∠ACD+∠ACF=30°,
∴∠ECF=∠ECA-∠ACF=60°-∠ACF=60°-(30°-∠ACD)=30°+∠ACD,
如图1,

延长AD,在AD上截取AD=DK,连接CK,
∵AD⊥BC,
∴∠ACD=∠KCD,CA=CK
∴∠FCK=∠FCD+∠KCD=∠ACF+∠ACD+∠KCD=30°+∠KCD=30°+∠ACD,
∴∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
|
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FD-AF;
(2)②结论:EF=2FA-FD,
如图2,

同(1)的方法得出∠FCK=∠ECF,
∵AC=CE,AC=CK,
∴CK=CE,
在△CFE和△CFK中,
|
∴△CFE≌△CFK,
∴FE=FK=FD+DK,
∵AD=DK,
∴FE=2FA-FD;
看了 己知:在等腰三角形ABC中,...的网友还看了以下:
(a^2-b^2)+4(b-1)怎么算啊已知:a=1/5x+20,b=1/5x+19,c=1/5x 2020-05-17 …
x的方程(m+5)*2-(2m-5)+m-8=0的两根,(1)求m的值;(2)求三角形ABC的三边 2020-05-22 …
第一题:设A=(0,1],B=[-1,0],求A∩B第二题:设A={1,2,3,4,5,6,7,8 2020-05-22 …
银行呆帐贷款余额与各项贷款余额之比不得超过___________。A.8%B.2%C.5%D.6% 2020-05-27 …
一道数学题,关于勾股定理,在解答"判断由线段长分别为6/5,2,8/5组成的三角形是不是直角三角形 2020-06-10 …
1.已知a+b+c=0,a^2+b^2+c^=1,求:①ab+bc+ac的值②a^4+b^4+c^ 2020-07-09 …
若a,b,c互不相等,求证关于x的方程(a^2+b^2+c^2)X^2+2(a+b+c)X+3=0 2020-08-01 …
直接写口数c.6÷c.6=6.3×c.四=12.五×c.8=1c÷c.五=c.8÷c.c4=c.42 2020-10-31 …
一、cos20度cos40度cos80度的值为:A.1/16,B.1/8,C1/4,D1/2.二、函 2020-10-31 …
各种有关印刷和PS的问题~2.(1分)\x05位图模式下图像的颜色有()种.(A)8(B)3(C)2 2020-11-07 …