早教吧作业答案频道 -->数学-->
28、(1)能把平行四边形分成面积相等的两部分的直线有条,它们的共同特点是.(2)如图,已知:AB∥CD∥FE,AF∥BC∥DE、求作一条直线,将这个图形分成面积相等的两部分、要求:
题目详情
28、(1)能把平行四边形分成面积相等的两部分的直线有____条,它们的共同特点是____.
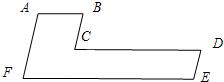
(2)如图,已知:AB∥CD∥FE,AF∥BC∥DE、求作一条直线,将这个图形分成面积相等的两部分、要求:对分法的合理性进行说明,并在图中作出分法的示意图(保留作图痕迹).
(3)自己设计一个图形A(由至少两个基本的中心对称图形B、C组成),并做出可以将图形A面积分成相等两部分的直线.
(2)如图,已知:AB∥CD∥FE,AF∥BC∥DE、求作一条直线,将这个图形分成面积相等的两部分、要求:对分法的合理性进行说明,并在图中作出分法的示意图(保留作图痕迹).

(3)自己设计一个图形A(由至少两个基本的中心对称图形B、C组成),并做出可以将图形A面积分成相等两部分的直线.
▼优质解答
答案和解析
分析:(1)根据平行四边形的性质可知能把平行四边形分成面积相等的两部分的直线有无数条,它们的共同特点是均经过两条对角线的交点.(2)延长BC交EF于点M,连接AM、BF交于点P,连接CE、DM交于点Q,P、Q分别为四边形ABMF、四边形CDEM的对称中心,直线PQ即为所求.(3)根据题意先作出图形,分别找到两个图形的对称中心,连接即可.(1)无数.均经过两条对角线的交点.(2)延长BC交EF于点M,连接AM、BF交于点P,连接CE、DM交于点Q,过P、Q的直线将这个图形分成面积相等的两部分,因为PQ既将平行四边形ABMF的面积平分,又将平行四边形CDEM的面积平分,所以直线PQ即为所求.(3)如图所示:点评:本题考查了中心对称图形的性质:经过对称中心的直线将中心对称图形分成面积相等的两部分.
看了 28、(1)能把平行四边形分...的网友还看了以下:
中心在原点O,焦点F1、F2在x轴上的椭圆E经过C(2,2),且CF1•CF2=2.(1)求椭圆E 2020-05-15 …
已知椭圆E:x^2/a^2+y^2/b^2=1(a>b>0)的离心率为1/2,直线x=2被椭圆E截 2020-05-16 …
已知关于x的多项式ax的4次方+bx的3次方+cx的2次方+dx+e的三次方其中ABCD为互不相等 2020-05-16 …
已知三角形abc根据要求在边bc上求作一点d使得点d到abac的距离相等在边ab上求一点e使得点e 2020-06-20 …
设矩阵A与B相似,求|A^2+E|设矩阵A与[-100020002]相似,求|A^2+E|求具体过 2020-07-13 …
如图三角形ABC中,D,E分别为AC,BC边上的点,BC平行于DE,BC=3,AC=4,AB=5, 2020-07-22 …
设定圆(x+根号3)^2+y^2=16,动圆N过点F(根号3,0)且与圆M相切,记圆心N的轨迹为E 2020-07-26 …
已知P是圆C:x2+y2=4上的动点,P在x轴上的射影为P′,点M满足PM=MP′,当P在圆上运动 2020-07-30 …
动圆G与圆Q1:X2+Y2+2X=0外切,同时与圆O2:X2+Y2-2X-8=0内切,设动圆圆心G 2020-07-31 …
limn→+00,e的n分之1次方*(1-e)除以n*(1-e的n分之1次方)=e-1是怎么算来的? 2020-12-17 …