如图，正方形ABCD中，点E，F分别在边CD，BC上，且∠EAF=45°，BD分别交AE，AF于点M，N，以点A为圆心，AB长为半径画弧BD．下列结论：①DE+BF=EF；②BN2+DM2=MN2；③△AMN∽△AFE；④BD与EF相切；⑤EF∥MN

Question

如图，正方形ABCD中，点E，F分别在边CD，BC上，且∠EAF=45°，BD分别交AE，AF于点M，N，以点A为圆心，AB长为半径画弧BD．下列结论：①DE+BF=EF；②BN²+DM²=MN²；③△AMN∽△AFE；④

BD

与EF相切；⑤EF∥MN．其中正确结论的个数是（　　）

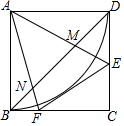
A. 5个

B. 4个

C. 3个

D. 2个

Answer 1

延长CB到G，使BG=DE，连接AG．
在△ABG和△ADE中，

AD=AB

∠D=∠ABG

DE=BG

，
∴△ABG≌△ADE，
∴AG=AE，∠DAE=∠BAG，
又∵∠EAF=45°，∠DAB=90°，
∴∠DAE+∠BAF=45°
∴∠GAF=∠EAF=45°．
在△AFG和△AFE中，

AE=AG

∠GAF=∠EAF

AF=AF

，
∴△AFG≌△AFE，
∴GF=EF=BG+BF，
又∵DE=BG，
∴EF=DE+BF；故①正确；
在AG上截取AH=AM．
在△AHB和△AMD中，

AD=AB

∠HAB=∠MAD

AH=AM

，
∴△AHB≌△AMD，
∴BH=DM，∠ABH=∠ADB=45°，
又∵∠ABD=45°，
∴∠HBN=90°．
∴BH²+BN²=HN²．
在△AHN和△AMN中，

AM=AH

∠HAN=∠MAN

AN=AN

，
∴△AHN≌△AMN，
∴MN=HN．
∴BN²+DM²=MN²；故②正确；
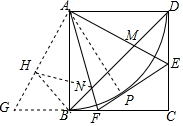
∵AB∥CD，
∴∠DEA=∠BAM．
∵∠AEF=∠AED，∠BAM=180°-∠ABM-∠AMN=180°-∠MAN-∠AMN=∠AND，
∴∠AEF=∠ANM，
又∠MAN=∠FAE，
∴△AMN∽△AFE，故③正确；
过A作AP⊥EF于P，
∵∠AED=∠AEP，AD⊥DE，
∴AP=AD，
∴

BD

与EF相切；故④正确；
∵∠ANM=∠AEF，而∠ANM不一定等于∠AMN，
∴∠AMN不一定等于∠AEF，
∴MN不一定平行于EF，故⑤错误，
故选B．