早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.(1)求证:△AED∽△ABC;(2)连接BD,判断四边形AEBD的形状并证明.
题目详情
如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
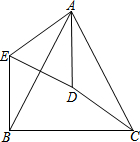
(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.

(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
▼优质解答
答案和解析
证明:(1)∵△ADC 绕点A顺时针旋转得到△AEB,
∴△ADC≌△AEB.
∴∠BAE=∠CAD,AE=AD.
∴∠DAE=∠CAB.
∵AB=AC,
∴
=
.
∴△AED∽△ABC.
(2)四边形AEBD是菱形.
∵D是△ABC的外心,
∴DB=DA=DC.
又∵△ADC≌△AEB,
∴AE=AD,BE=DC.
∴DB=DA=BE=AE.
∴四边形AEBD是菱形.
∴△ADC≌△AEB.
∴∠BAE=∠CAD,AE=AD.
∴∠DAE=∠CAB.
∵AB=AC,
∴
| AE |
| AB |
| AD |
| AC |
∴△AED∽△ABC.
(2)四边形AEBD是菱形.
∵D是△ABC的外心,
∴DB=DA=DC.
又∵△ADC≌△AEB,
∴AE=AD,BE=DC.
∴DB=DA=BE=AE.
∴四边形AEBD是菱形.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于 2020-03-30 …
矢量代数 证明 “已知a×b = c×d,a×c = b×d,证明a - d与b - c共线.” 2020-04-05 …
向量数量积分配律证明向量数量积分配律a•(b+c)=a•b+a•c,(a+b)•(c+d)=a•c 2020-06-19 …
1.已知点A(0,1),B(1,0),c(1,2)D(2,1),试判断向量A到B和C到D的位置关系 2020-06-21 …
数学厉害的进来1求证a²+3b²≥2b(a+b)2,求证a²+b²+2≥2a+2b3,已知a≠2, 2020-07-09 …
已知,角AOB等于90度,OM是叫AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角分别 2020-07-24 …
1如果下雨,春游就会改期;如果没有球赛,春游就不会改期.结果没有比赛,所以没有下雨.证明上述判断正 2020-07-27 …
柯西不等式等号成立条件?并证明(a方+b方)(c方+d方)≥(ac+bd)方等号成立条件:ac=b 2020-08-01 …
实验室有一种电池,因为时间久远难以辨认正负极,如图为设计的几种判断正负极的方案.选取的器材均能保证了 2020-12-10 …
选出填入下列空白处最恰当的一项是:()对欧元的问世及其影响的判断还有待时间和实践来()。A.证明B. 2020-12-22 …