早教吧作业答案频道 -->数学-->
在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,
题目详情
在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.
…
请你参考上面的想法,帮助小宇证明∠APE=2∠MAD.(一种方法即可)
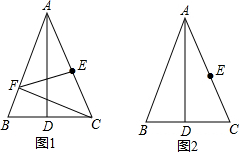
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.
…
请你参考上面的想法,帮助小宇证明∠APE=2∠MAD.(一种方法即可)

▼优质解答
答案和解析
(1)证明:∵AB=AC,AD为BC边上的高,∠BAD=20°,
∴∠BAC=2∠BAD=40°.
∵CF⊥AB,
∴∠AFC=90°.
∵E为AC中点,
∴EF=EA=
AC.
∴∠AFE=∠BAC=40°.
(2)①Ⅰ、当点P在边AB上时,补全图形如图1,
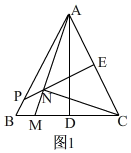
Ⅱ、当点P在AB的延长线上时,补全图形如图2,
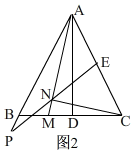
②Ⅰ、当点P在边AB上时,
证明:想法1:如图3,
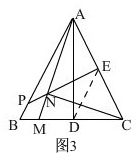
连接DE.
∵AB=AC,AD为BC边上的高,
∴D为BC中点.
∵E为AC中点,
∴ED∥AB,
∴∠PED=∠APE.
【∵∠ADC=90°,E为AC中点,
∴AE=DE=CE=
AC.
同理可证AE=NE=CE=
AC.
∴AE=NE=CE=DE.
∴A,N,D,C在以点E为圆心,AC为直径的圆上,】
∴∠PED=2∠MAD.
∴∠APE=2∠MAD.
【】里面的学过四点共圆的判断方法的可以换成:
∵∠ADC=∠ANC=90°,
∴点A,N,D,C四点共圆;
想法2:设∠MAD=α,∠DAC=β,
∵CN⊥AM,
∴∠ANC=90°.
∵E为AC中点,
∴AE=NE=
AC.
∴∠ANE=∠NAC=∠MAD+∠DAC=α+β.
∴∠NEC=∠ANE+∠NAC=2α+2β.
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=2β.
∴∠APE=∠PEC-∠BAC=2α.
∴∠APE=2∠MAD.
Ⅱ、当点P在AB的延长线上时,
证明:想法1:如图4,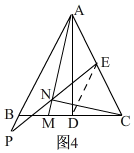
连接DE.
∵AB=AC,AD为BC边上的高,
∴D为BC中点.
∵E为AC中点,
∴ED∥AB,
∴∠PED=∠APE.
∵∠ADC=90°,E为AC中点,
∴AE=DE=CE=
AC.
同理可证AE=NE=CE=
AC.
∴AE=NE=CE=DE.
∴A,N,D,C在以点E为圆心,AC为直径的圆上.
∴∠PED=2∠MAD.
∴∠APE=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,
∵CN⊥AM,
∴∠ANC=90°.
∵E为AC中点,
∴AE=NE=
AC.
∴∠ANE=∠NAC=∠MAD+∠DAC=α+β.
∴∠NEC=∠ANE+∠NAC=2α+2β.
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=2β.
∴∠APE=∠PEC-∠BAC=2α.
∴∠APE=2∠MAD.
∴∠BAC=2∠BAD=40°.
∵CF⊥AB,
∴∠AFC=90°.
∵E为AC中点,
∴EF=EA=
| 1 |
| 2 |
∴∠AFE=∠BAC=40°.
(2)①Ⅰ、当点P在边AB上时,补全图形如图1,

Ⅱ、当点P在AB的延长线上时,补全图形如图2,

②Ⅰ、当点P在边AB上时,
证明:想法1:如图3,

连接DE.
∵AB=AC,AD为BC边上的高,
∴D为BC中点.
∵E为AC中点,
∴ED∥AB,
∴∠PED=∠APE.
【∵∠ADC=90°,E为AC中点,
∴AE=DE=CE=
| 1 |
| 2 |
同理可证AE=NE=CE=
| 1 |
| 2 |
∴AE=NE=CE=DE.
∴A,N,D,C在以点E为圆心,AC为直径的圆上,】
∴∠PED=2∠MAD.
∴∠APE=2∠MAD.
【】里面的学过四点共圆的判断方法的可以换成:
∵∠ADC=∠ANC=90°,
∴点A,N,D,C四点共圆;
想法2:设∠MAD=α,∠DAC=β,
∵CN⊥AM,
∴∠ANC=90°.
∵E为AC中点,
∴AE=NE=
| 1 |
| 2 |
∴∠ANE=∠NAC=∠MAD+∠DAC=α+β.
∴∠NEC=∠ANE+∠NAC=2α+2β.
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=2β.
∴∠APE=∠PEC-∠BAC=2α.
∴∠APE=2∠MAD.
Ⅱ、当点P在AB的延长线上时,
证明:想法1:如图4,

连接DE.
∵AB=AC,AD为BC边上的高,
∴D为BC中点.
∵E为AC中点,
∴ED∥AB,
∴∠PED=∠APE.
∵∠ADC=90°,E为AC中点,
∴AE=DE=CE=
| 1 |
| 2 |
同理可证AE=NE=CE=
| 1 |
| 2 |
∴AE=NE=CE=DE.
∴A,N,D,C在以点E为圆心,AC为直径的圆上.
∴∠PED=2∠MAD.
∴∠APE=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,
∵CN⊥AM,
∴∠ANC=90°.
∵E为AC中点,
∴AE=NE=
| 1 |
| 2 |
∴∠ANE=∠NAC=∠MAD+∠DAC=α+β.
∴∠NEC=∠ANE+∠NAC=2α+2β.
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=2β.
∴∠APE=∠PEC-∠BAC=2α.
∴∠APE=2∠MAD.
看了 在锐角△ABC中,AB=AC...的网友还看了以下:
等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、 2020-06-23 …
若正方体ABCD-A1B1C1D1的棱长为a,点M、N分别是棱AA1,CC1的中点,求四棱锥A-M 2020-07-09 …
如图所示,用长为L的绝缘细线拴住一个质量为m,带电荷量为q的小球,线的另一端拴在水平向右的匀强电场 2020-07-11 …
如图所示为圆弧形固定光滑轨道,a点切线方向与水平方向夹角53°,b点切线方向水平。一小球以水平初速度 2020-11-01 …
在平面直角坐标系中,直线y=kx+3交x正半轴于点B,交y轴于点A,点M(1,1)在△ABO内部,连 2020-11-01 …
若有理数m>n,在数轴上点M表示数m,点N表示数n,则()A.点M在点N的右边B.点M在点N的左边C 2020-11-20 …
如图,有一半径为R=0.3m的半圆形细管AB,将其固定在竖直墙面上并使其轨道平面在竖直平面内,且B端 2020-11-26 …
如图,有一半径为R=0.3m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平.一个可视为质点 2020-11-26 …
如图,有一半径为R=0.3m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平.一个可视为质点 2020-11-26 …
点P是双曲线x2a2-y2b2=1(a>0,b>0)的右支上一点,其左,右焦点分别为F1,F2,直线 2020-12-31 …